带有非精确线搜索的 BB 步长梯度下降法
考虑无约束优化问题:
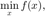
其中目标函数 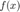 是可微的。
是可微的。
对于可微的目标函数 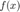 ,梯度下降法通过使用如下重复如下迭代格式
,梯度下降法通过使用如下重复如下迭代格式

求解 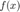 的最小值,其中
的最小值,其中 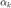 为第
为第  步的步长。
步的步长。
令 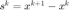 ,
, 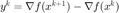 ,定义两种 BB 步长,
,定义两种 BB 步长, 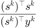 和
和 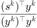 。在经验上,采用 BB 步长的梯度法往往可以取得比固定步长更好的结果。
。在经验上,采用 BB 步长的梯度法往往可以取得比固定步长更好的结果。
目录
初始化和迭代准备
输入信息:  为迭代的初始值(可以为一个矩阵),函数 fun 依次返回给定点的函数和梯度值, 以及给出参数的结构体 opt 。
为迭代的初始值(可以为一个矩阵),函数 fun 依次返回给定点的函数和梯度值, 以及给出参数的结构体 opt 。
输出信息:  为求得的最优点,
为求得的最优点,  为该点处梯度, out 为一个包含其它信息的结构体。
为该点处梯度, out 为一个包含其它信息的结构体。
- out.nfe :函数 fun 调用的次数
- out.fval0 :初始点函数值
- out.msg :标记是否达到收敛
- out.nrmG :退出时该点处梯度的F-范数
- out.itr :迭代步数。
function [x, g, out]= fminGBB(x, fun, opts, varargin)
该算法实现对于给定函数 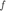 (由 fun 定义)的梯度下降法,其使用以 BB 步长为初始步长的非精确线搜索。
(由 fun 定义)的梯度下降法,其使用以 BB 步长为初始步长的非精确线搜索。
从输入的结构体中读取参数或采取默认参数。
- opts.xtol :针对自变量的停机准则
- opts.gtol :针对梯度的停机准则
- opts.ftol :针对函数值的停机准则
- opts.tau :默认步长(第一步或 BB 步长失效时采用默认步长)
- opts.rhols :线搜索准则中下降量参数
- opts.eta :步长衰减率
- opts.gamma : Zhang & Hager 非单调线索准则参数
- opts.maxit :最大迭代步数
- opts.record :输出的详细程度,当为 0 时不进行输出,大于等于 1 时输出每一步信息,为 10 时额外记录每一步的函数值
if ~isfield(opts, 'xtol'); opts.xtol = 0; end if ~isfield(opts, 'gtol'); opts.gtol = 1e-6; end if ~isfield(opts, 'ftol'); opts.ftol = 0; end if ~isfield(opts, 'tau'); opts.tau = 1e-3; end if ~isfield(opts, 'rhols'); opts.rhols = 1e-4; end if ~isfield(opts, 'eta'); opts.eta = 0.2; end if ~isfield(opts, 'gamma'); opts.gamma = 0.85; end if ~isfield(opts, 'maxit'); opts.maxit = 1000; end if ~isfield(opts, 'record'); opts.record = 0; end
复制参数。
xtol = opts.xtol; ftol = opts.ftol; gtol = opts.gtol; maxit = opts.maxit; rhols = opts.rhols; eta = opts.eta; gamma = opts.gamma; record = opts.record;
初始化。
计算初始点  处的函数值和梯度。
处的函数值和梯度。
[n,p] = size(x);
[f,g] = feval(fun, x, varargin{:});
out.nfe = 1;
out.fval0 = f;
nrmG = norm(g, 'fro');
线搜索参数。
Q = 1; Cval = f; tau = opts.tau;
当 record 大于等于 1 时为每一步的输出打印表头,每一列分别为:当前迭代步、当前步长、当前步函数值、梯度范数、相对  变化量、相对函数值变化量、线搜索次数。
变化量、相对函数值变化量、线搜索次数。
if (record >= 1) fprintf('----------- fminBB ----------- \n'); fprintf('%4s \t %6s \t %8s \t %5s \t %7s \t %7s \t %3s \n', ... 'Iter', 'tau', 'f(X)', 'nrmG', 'XDiff', 'FDiff', 'ls-Iter'); end
当 record 为 10 时,额外记录每一步的函数值。
if record == 10; out.fvec = f; end
初始化求解结果为超过最大迭代次数(即在达到最大迭代步数过程中没有满足任何针对自变量、函数值、梯度的停机准则)
out.msg = 'exceed max iteration';
迭代主循环
以 maxit 为最大迭代次数。在每一步迭代开始时复制前一步的  、函数值和梯度。
、函数值和梯度。
for itr = 1 : maxit
xp = x; fp = f; gp = g;
非精确线搜索。初始化线搜索次数 nls = 1。 满足线搜索准则(Zhang & Hager) 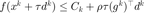 或进行超过 10 次步长衰减后退出线搜索,否则以
或进行超过 10 次步长衰减后退出线搜索,否则以  的比例对步长进行衰减。
的比例对步长进行衰减。
nls = 1;
while 1
x = xp - tau*gp;
[f,g] = feval(fun, x, varargin{:}); out.nfe = out.nfe + 1;
if f <= Cval - tau*rhols*nrmG^2 || nls >= 10
break
end
tau = eta*tau;
nls = nls+1;
end
当 record 为 10 时,记录每一步迭代的函数值。
if record == 10; out.fvec = [out.fvec; f]; end
nrmG 为  处的梯度范数,|XDiff| 表示
处的梯度范数,|XDiff| 表示  与上一步迭代
与上一步迭代  之前的相对变化, FDiff 表示函数值的相对变化,当 record 大于等于 1 时将这些信息输出。
之前的相对变化, FDiff 表示函数值的相对变化,当 record 大于等于 1 时将这些信息输出。
nrmG = norm(g, 'fro'); s = x - xp; XDiff = norm(s,'fro')/sqrt(n); FDiff = abs(fp-f)/(abs(fp)+1); if (record >= 1) fprintf('%4d \t %3.2e \t %7.6e \t %3.2e \t %3.2e \t %3.2e \t %2d\n', ... itr, tau, f, nrmG, XDiff, FDiff, nls); end
判断是否收敛,当下列停机准则至少一个被满足时停止迭代,并记录 out.msg 为收敛: (1)相对的  和函数值的相对变化量均小于给定的阈值;(2)当前梯度的范数小于给定的阈值。
和函数值的相对变化量均小于给定的阈值;(2)当前梯度的范数小于给定的阈值。
if ( XDiff < xtol && FDiff < ftol ) || nrmG < gtol out.msg = 'converge'; break; end
BB 步长的计算,以 BB 步长作为线搜索的初始步长。令 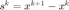 ,
, 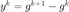 , 这里在偶数与奇数步分别对应
, 这里在偶数与奇数步分别对应 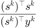 和
和 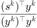 两个 BB 步长,当
两个 BB 步长,当 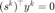 时使用默认步长。
时使用默认步长。
y = g - gp;
sy = abs(iprod(s,y)); tau = opts.tau;
if sy > 0
if mod(itr,2)==0; tau = abs(sum(sum(s.*s)))/sy;
else tau = sy/abs(sum(sum(y.*y))); end
限定在 ![$[10^{-20},10^{20}]$](fminGBB_eq07485874820074819537.png) 中。
中。
tau = max(min(tau, 1e20), 1e-20);
end
计算 (Zhang & Hager) 线搜索准则中的递推常数,其满足 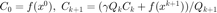 ,序列
,序列 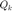 满足
满足  。
。
Qp = Q; Q = gamma*Qp + 1; Cval = (gamma*Qp*Cval + f)/Q;
end
记录输出。
out.nrmG = nrmG; out.fval = f; out.itr = itr;
end
辅助函数
矩阵形式的内积。为了在复数域上良定义,取实部。
function a = iprod(x,y) a = real(sum(sum(x.*y))); end
应用实例
我们将在 实例:Tikhonov 正则化模型用于图片去噪 展示如上的算法在图片去噪问题中的应用。
此页面的源代码请见: fminGBB.m。
版权声明
此页面为《最优化:建模、算法与理论》、《最优化计算方法》配套代码。 代码作者:文再文、刘浩洋、户将,代码整理与页面制作:杨昊桐。
著作权所有 (C) 2020 文再文、刘浩洋、户将