LASSO 问题的原始-对偶混合梯度 (PDHG) 算法

考虑 LASSO 问题

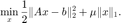
$\displaystyle\min_x \frac{1}{2}\|Ax-b\|_2^2 + \mu \|x\|_1.$

利用连续化策略和原始-对偶混合梯度算法优化该问题。该算法被外层连续化策略调用，在连续化策略下完成某一固定正则化系数的内层迭代优化。

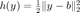原始-对偶混合梯度 (Primal Dual Hybird Gradient, PDHG) 算法在每一步迭代同时考虑原始变量和对偶变量的更新。对于上述 LASSO 问题，将其转化为鞍点问题，记 $f(x)=\mu\|x\|_1$ 和 $h(y)=\frac{1}{2}\|y-b\|_2^2$ ，问题等价于

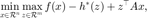
$\displaystyle\min_{x\in\mathcal{R}^n}\max_{z\in\mathcal{R}^m} f(x)-h^*(z)+z^\top Ax,$

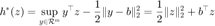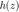其中 $\displaystyle h^*(z)=\sup_{y\in\mathcal{R}^m}y^\top z-\frac{1}{2}\|y-b\|_2^2= \frac{1}{2}\|z\|_2^2+b^\top z$ 为 $h(z)$ 的共轭函数。

应用 PDHG，得到迭代格式

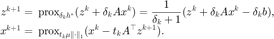
$\begin{array}{rl} z^{k+1}=&\hspace{-0.5em}\displaystyle\mathrm{prox}_{\delta_kh^*}(z^k+\delta_kAx^k) =\frac{1}{\delta_k+1}(z^k+\delta_kAx^k-\delta_kb),\\ x^{k+1}=&\hspace{-0.5em}\displaystyle\mathrm{prox}_{t_k\mu\|\cdot\|_1}(x^k-t_kA^\top z^{k+1}). \end{array}$

利用 Chambolle-Pock 算法格式，增加一步外推，则为

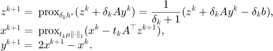
$\begin{array}{rl} z^{k+1}=&\hspace{-0.5em}\displaystyle\mathrm{prox}_{\delta_kh^*}(z^k+\delta_kAy^k) =\frac{1}{\delta_k+1}(z^k+\delta_kAy^k-\delta_kb), \\ x^{k+1}=&\hspace{-0.5em}\displaystyle\mathrm{prox}_{t_k\mu\|\cdot\|_1}(x^k-t_kA^\top z^{k+1}), \\ y^{k+1}=&\hspace{-0.5em}\displaystyle 2x^{k+1}-x^k. \end{array}$

初始化和迭代准备

函数在 LASSO 连续化策略下，完成内层迭代的优化。

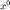输入信息： $A$ , $b$ ，当前内层迭代的正则化系数 $\mu$ ，迭代初始值 $x^0$ ，原问题对应的正则化系数 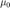$\mu_0$ ，以及提供各参数的结构体 opts 。

输出信息：迭代得到的解 $x$ 和结构体 out 。

out.fvec ：每一步迭代的原始目标函数值（对应于原问题的 $\mu_0$ ）
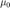out.fval ：迭代终止时的原始目标函数值（对应于原问题的 $\mu_0$ ）
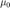out.nrmG ：迭代终止时的梯度范数
out.tt ：运行时间
out.itr ：迭代次数
out.flag ：标记是否达到收敛

function [x, out] = LASSO_pdhg_inn(x0, A, b, mu, mu0, opts)

从输入的结构体 opts 中读取参数或采取默认参数。

opts.maxit ：最大迭代次数
opts.ftol ：针对函数值的停机准则，当相邻两次迭代函数值之差小于该值时认为该条件满足
opts.gtol ：针对梯度的停机准则，当当前步梯度范数小于该值时认为该条件满足
opts.verbose ：不为 0 时输出每步迭代信息，否则不输出
opts.alpha0 ：初始步长
opts.cp ：是否使用 Chambolle-Pock 算法

if ~isfield(opts, 'maxit'); opts.maxit = 200; end
if ~isfield(opts, 'ftol'); opts.ftol = 1e-8; end
if ~isfield(opts, 'gtol'); opts.gtol = 1e-6; end
if ~isfield(opts, 'verbose'); opts.verbose = 0; end
if ~isfield(opts, 'alpha0'); opts.alpha0 = 1e-3; end
if ~isfield(opts, 'cp'); opts.cp = 0; end

初始设定。

设置输出的结构体 out。

out = struct();

以 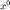$x^0$ 为迭代初始点。

x = x0;

对 z 的步长 delta=1。

t1 = 1;

对 x 的步长 alpha 为 opts.alpha0。

alpha = opts.alpha0;
tt = tic;

计算辅助变量， f 计算对于原始正则化系数 mu_0 的目标函数值。

Ax = A*x;
r = Ax - b;
f = .5*norm(r,2)^2 + mu0*norm(x,1);
out.fvec = f;

初始时刻 z^0=Ax^0-b。

z = r;

迭代主循环

内层循环，以 opts.maxit 为最大迭代次数。开始时记录上一步的函数值。

for k = 1:opts.maxit
    fp = f;

对 $z$ 的更新，对应于一步近似点法。迭代格式

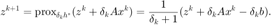
$z^{k+1}=\mathrm{prox}_{\delta_kh^*}(z^k+\delta_kAx^k) =\frac{1}{\delta_k+1}(z^k+\delta_kAx^k-\delta_kb).$

    z = (-b + 1/t1*(z+t1*Ax))/(1+1/t1);

对 $x$ 的更新， $x^{k+1}=\mathrm{prox}_{\alpha_k\mu\|x\|_1}(x^k-t_kA^\top z^{k+1})$ 。注意到如果使用 Chambolle-Pock 算法，需要记录上一步的 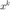$x^k$ 。

    xp = x;
    x = prox(xp - alpha*(A'*z), alpha*mu);

如果使用 Chambolle-Pock 算法，在原始 PDHG 算法基础上增加一个外推步 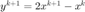$y^{k+1}=2x^{k+1}-x^{k}$ 。在 $z$ 的更新中以外推一步得到的 $y$ 替代 $x$ 。

    if opts.cp
        y = 2*x - xp;
    else
        y = x;
    end

一步迭代后，更新函数值和梯度（一步近似点梯度法估计）的范数，记录函数值。

    Ax = A*y;
    Axb = Ax - b;
    f = .5*norm(Axb,2)^2 + mu0*norm(x,1);
    nrmG = norm(y - prox(y - A'*Axb, mu));
    out.fvec= [out.fvec, f];

当 verbose 不为 0 时，输出迭代信息。

    if opts.verbose
        fprintf('itr: %4d\t fval: %e \t nrmG: %.1e \n', k, f, nrmG);
    end

内层迭代的停机准则，当函数值变化小于阈值或者梯度（以投影梯度法估计）模长小于阈值时，认为达到收敛，退出内层迭代。当退出循环时，向外层迭代（连续化策略）报告内层迭代的退出方式，当达到最大迭代次数退出时， out.flag 记为 1，否则为达到收敛，记为 0。这个指标用于判断是否进行正则化系数的衰减。

    if abs(f-fp) < opts.ftol || nrmG < opts.gtol
        break;
    end
end

if k == opts.maxit
    out.flag = 1;
else
    out.flag = 0;
end

记录内层迭代的输出。

out.fval = f;
out.itr = k;
out.tt = toc(tt);

end

辅助函数

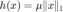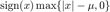函数 $h(x)=\mu\|x\|_1$ 对应的邻近算子 $\mathrm{sign}(x)\max\{|x|-\mu,0\}$ 。

function y = prox(x, mu)
y = max(abs(x) - mu, 0);
y = sign(x) .* y;
end

参考页面

该函数由连续化策略调用，关于连续化策略参见 LASSO问题连续化策略。我们在页面实例：利用原始-对偶混合梯度算法解 LASSO 问题中构建一个 LASSO 问题并展示该算法在其中的应用。

此页面的源代码请见： LASSO_pdhg_inn.m。

版权声明