实例：利用梯度法解 LASSO 问题

考虑 LASSO 问题：

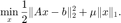
$\displaystyle \min_x \frac{1}{2}\|Ax-b\|_2^2+\mu\|x\|_1.$

利用 Huber 光滑化方法通过以光滑函数逼近 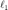$\ell_1$ -范数，以在得到的可微函数上利用梯度下降法对原问题近似求解。我们在此展示 Huber 光滑化梯度法的应用。

构建 LASSO 问题

设定随机种子。

clear;
seed = 97006855;
ss = RandStream('mt19937ar','Seed',seed);
RandStream.setGlobalStream(ss);

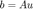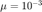生成随机的矩阵 $A$ 和向量 $u$ 以使得 $b=Au$ 。第一次实验，给定正则化系数 $\mu=10^{-3}$ 。

m = 512;
n = 1024;
A = randn(m, n);
u = sprandn(n, 1, 0.1);
b = A * u;
mu = 1e-3;

$L$ 为 $A^\top A$ 的最大特征值，用于步长的选取。

L = eigs(A'*A, 1);
x0 = randn(n, 1);

求解 LASSO 问题

首先在更严格的收敛条件下进行试验，将收敛时得到的函数值作为真实的最优值的参考 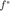$f^*$ 。

opts = struct();
opts.method = 'grad_huber';
opts.verbose = 0;
opts.maxit = 4000;
opts.ftol = 1e-8;
opts.alpha0 = 1 / L;

添加连续化策略函数所在的目录。

addpath('../LASSO_con')
[x, out] = LASSO_con(x0, A, b, mu, opts);
f_star = min(out.fvec);

Huber 光滑化的梯度法（包括 BB 步长和非精确线搜索）， out.fvec 记录迭代过程中的目标函数值。

opts.verbose = 0;
opts.maxit = 400;
if opts.verbose
    fprintf('mu=1e-3\n');
end
[x, out] = LASSO_con(x0, A, b, mu, opts);
data1 = (out.fvec - f_star)/f_star;
k1 = min(length(data1),400);
data1 = data1(1:k1);

将 $\mu$ 修改为 1e-2 重复实验。

mu = 1e-2;
opts = struct();
opts.method = 'grad_huber';
opts.verbose = 0;
opts.maxit = 4000;
opts.ftol = 1e-8;
opts.alpha0 = 1 / L;
[x, out] = LASSO_con(x0, A, b, mu, opts);
f_star = min(out.fvec);

opts.verbose = 0;
opts.maxit = 400;
if opts.verbose
    fprintf('\nmu=1e-2\n');
end
[x, out] = LASSO_con(x0, A, b, mu, opts);
data2 = (out.fvec - f_star)/f_star;
k2 = min(length(data2),400);
data2 = data2(1:k2);

结果可视化

可视化优化过程：观察目标函数值随迭代次数的变化。同时展示求解优化问题得到的解各个分量的大小。

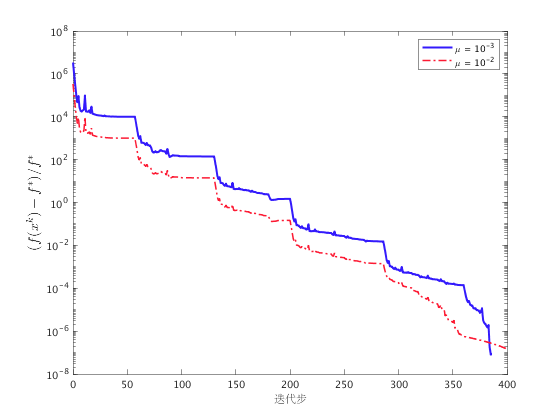
fig = figure;
semilogy(0:k1-1, data1, '-', 'Color',[0.2 0.1 0.99], 'LineWidth',2);
hold on
semilogy(0:k2-1, data2, '-.','Color',[0.99 0.1 0.2], 'LineWidth',1.5);
legend('\mu = 10^{-3}', '\mu = 10^{-2}');
ylabel('$(f(x^k) - f^*)/f^*$', 'fontsize', 14, 'interpreter', 'latex');
xlabel('迭代步');
print(fig, '-depsc','grad.eps');

figure;
subplot(2, 1, 1);
plot(u, 'Color',[0.2 0.1 0.99], 'Marker', 'x', 'LineStyle', 'none');
xlim([1, 1024]);
title('精确解');

subplot(2, 1, 2);
plot(x, 'Color',[0.2 0.1 0.99], 'Marker', 'x', 'LineStyle', 'none');
xlim([1, 1024]);
title('梯度法解');

saveas(gcf, 'solu-smoothgrad.eps');

结果分析

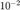采取连续化策略之后，光滑化梯度法在 400 步左右收敛到了最小值。注意到在 $\mu$ 减小到 $10^{-2}$ 之前，两次优化的过程是完全相同的（图像不重合而是平行是由于对应的最小值不同），并且在每次 $\mu$ 减小后，函数值都有迅速的下降。这一现象与采用连续化策略的其它优化方法是完全相同的。

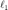另外，右图展示解的分量大小，其大部分的分量集中在 $0$ 的附近。这证实通过 $\ell_1$ -范数正则，算法确实得到了稀疏性良好的解。

参考页面

Huber 光滑化梯度法的算法实现参考 Huber 光滑化梯度法，连续化策略参考 LASSO 问题连续化策略。

此页面的源代码请见： demo.m。

版权声明

此页面为《最优化：建模、算法与理论》、《最优化计算方法》配套代码。代码作者：文再文、刘浩洋、户将，代码整理与页面制作：杨昊桐。