实例：利用 L-BFGS 算法求解基追踪问题

考虑基追踪问题

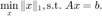
$\displaystyle \min_x \|x\|_1, \mathrm{s.t.}\ Ax = b.$

通过计算可知该问题的对偶问题的无约束优化形式不是可微的（因为原问题目标函数不是强凸的，读者可以自行推导验证）。这里，考虑它的正则化问题

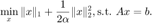
$\displaystyle \min_x \|x\|_1 + \frac{1}{2\alpha} \|x\|_2^2, \mathrm{s.t.}\ Ax = b.$

通过计算，其对偶问题为：

$\displaystyle \min_y -b^\top y + \frac{\alpha}{2}\|A^\top y - \mathcal{P}_{[-1,1]^n}(A^\top y) \|_2^2,$

目标函数在点 $x$ 处的梯度为：

$-b + \alpha A(A^\top y - \mathcal{P}_{[-1,1]^n}(A^\top y)).$

这里，利用 L-BFGS 算法求解对应的问题。

构建基追踪问题

设定随机种子。

clear;
seed = 97006855;
ss = RandStream('mt19937ar','Seed',seed);
RandStream.setGlobalStream(ss);

生成随机的矩阵 $A$ 和向量 $u$ 以使得 $b=Au$ 。

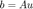m = 512;
n = 1024;
A = randn(m, n);
u = sprandn(n, 1, 0.1);
b = A * u;

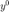$y^0$ 为迭代的初始点。

x0 = randn(n, 1);
y0 = A*x0 - b;

$\alpha$ 为正则化参数，当 $\alpha$ 足够大时，正则化问题的解就是原问题的解（可以参考教材相关章节）。 opts.m 为 L-BFGS 算法的记忆对存储数目。 bpdual 为正则化问题的对偶问题的目标函数（参见辅助函数）。

alpha = 5;
opts = struct();
opts.xtol = 1e-8;
opts.gtol = 1e-6;
opts.ftol = 1e-16;

opts.m  = 5;
opts.storeitr = 1;

fun = @(y) bpdual(y,A,b,alpha);
dist1 = [];
[y1, ~, ~, Out1]= fminLBFGS_Loop(y0, fun, opts);

如果算得对偶问题的解 $y$ ，利用如下格式构造出对应的 $x$ 。

$x=\alpha(A^\top y - \mathcal{P}_{[-1,1]^n}(A^\top y)).$

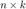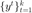out1.xitr 为一个 $n\times k$ 的矩阵，其中 $n$ 为对偶问题自变量 $y$ 的维度， $k$ 为迭代步数，该矩阵记录了 L-BFGS 算法的迭代过程 $\{y^t\}_{t=1}^k$ ，从 $y$ 中恢复出每一步对应的 $x$ 。

AtY = A'*Out1.xitr;
C = max(min(AtY, 1),-1);
D = AtY - C;
X = alpha*D;

L-BFGS 求得的基追踪问题的解。求解的可行度 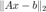$\|Ax-b\|_2$ 作为判断标准。 dist1 计算某一步迭代对应的 $x$ 与真实解 $x^*=u$ 的距离。

x1 = X(:,end);
feasi1 = norm(A*x1 - b);
for i = 1:size(X,2)
    dist1 = [dist1;norm(X(:,i) - u,2)];
end
k1 = length(dist1);

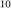将正则化系数 $\alpha$ 改为 $10$ ，其余不变，重复实验。

alpha = 10;
fun = @(y) bpdual(y,A,b,alpha);
dist2 = [];
[y2, ~, ~, Out2]= fminLBFGS_Loop(y0, fun, opts);

AtY = A'*Out2.xitr;
C = max(min(AtY, 1),-1);
D = AtY - C;
X = alpha*D;
for i = 1:size(X,2)
    dist2 = [dist2;norm(X(:,i) - u,2)];
end

x2 = X(:,end);
feasi2 = norm(A*x2 - b);
k2 = length(dist2);

结果可视化

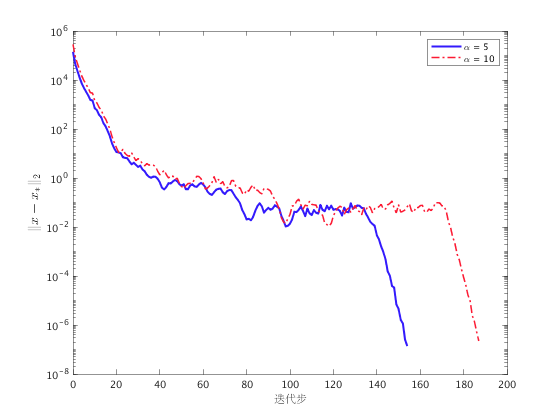
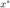可视化每一步迭代对应的 $x$ 与真实解 $x^*$ 之间的距离。

fig = figure;
semilogy(0:k1-1, dist1, '-', 'Color',[0.2 0.1 0.99], 'LineWidth',2);
hold on
semilogy(0:k2-1, dist2, '-.','Color',[0.99 0.1 0.2], 'LineWidth',1.5);
legend('\alpha = 5', '\alpha = 10');
ylabel('$\|x - x_*\|_2$', 'fontsize', 14, 'interpreter', 'latex');
xlabel('迭代步');
print(fig, '-depsc','bp_lbfgs.eps');

辅助函数

正则化问题的对偶问题的目标函数（及其梯度）。

function [f,g] = bpdual(y,A,b,alpha)

由 $y$ 构造出 $x$ ，并计算相应的误差。

Aty = A'*y;
c = max(min(Aty, 1),-1);
d = Aty - c;
x = alpha*d;

目标函数值和当前点处的梯度（ nargout表示当前函数在被调用时，需要的输出的个数，这里表示当输出个数大于1时计算梯度）。

f = -b'*y + alpha/2*norm(d,2)^2;

if nargout > 1
    g = -b + A*x;
end
end

结果分析

上图展示了基追踪问题在迭代过程中的误差变化情况，当 $\alpha=5$ 和 $\alpha=10$ 时，正则化问题的解均非常接近真正的解；并观察到，对于更大的正则化系数 $\alpha$ 得到的解的精确性更好。

同时，我们发现当接近最优解时，算法呈现接近线性的收敛速度。

参考页面

L-BFGS 算法，参见 L-BFGS 求解优化问题。该算法的另一个应用参考页面实例：L-BFGS 求解逻辑斯蒂回归问题。

此页面的源代码请见： demo_bp_lbfgs.m。

版权声明

此页面为《最优化：建模、算法与理论》、《最优化计算方法》配套代码。代码作者：文再文、刘浩洋、户将，代码整理与页面制作：杨昊桐。