编码衍射模型 LM 子问题的预条件（截断）共轭梯度算法

考虑LM 方程对应的无约束二次优化问题：

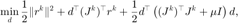
$\displaystyle\min_d \frac{1}{2}\|r^k\|^2+d^\top(J^k)^\top r^k +\frac{1}{2}d^\top\left((J^k)^\top J^k+\mu I\right)d,$

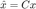利用预条件共轭梯度法进行近似求解。为了记号的方便，在下文我们用 $x$ 表示问题的自变量， $r$ 表示共轭梯度法中的残差变量。预条件共轭梯度法在共轭梯度法的基础上，引入 $\hat{x}=Cx$ 。因此，对于问题

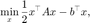
$\min_x \frac{1}{2}x^\top A x -b^\top x,$

采用预条件共轭梯度法等于使用共轭梯度法求解如下问题

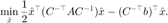
$\min_{\hat{x}}\frac{1}{2}\hat{x}^\top(C^{-\top}AC^{-1})\hat{x}-(C^{-\top}b)^\top\hat{x}.$

预条件共轭梯度法的迭代格式为（其中记 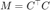$M=C^\top C$ ）

$\begin{array}{rl} \displaystyle Mz^{k}&\hspace{-0.5em}=r^{k}, \\ \displaystyle\beta_{k}&\hspace{-0.5em}= \displaystyle\frac{(r^{k})^\top z^{k}}{(r^{k-1})^\top z^{k-1}}, \\ \displaystyle p^{k}&\hspace{-0.5em}=z^{k}+\beta_{k} p^{k-1}, \\ \displaystyle\alpha_k &\hspace{-0.5em}= \displaystyle\frac{(r^k)^\top z^{k}}{(p^{k})^\top A p^k},\\ \displaystyle x^{k+1}&\hspace{-0.5em}=x^k+\alpha_k p^{k}, \\ \displaystyle r^{k+1}&\hspace{-0.5em}=r^k-\alpha_k Ap^{k}. \end{array}$

初始化和迭代准备

输入信息：当前迭代点 $z$ ，采样信号矩阵 $A$ ，观测模长 $y$ ，最大迭代次数 ite_max 和判断精度的标志 acu 。输出信息：返回LM 方程的解 $d$ (记为 solu )和包含迭代信息的结构体 info， info.ite 记录迭代次数， info.prod 记录矩阵向量积的次数。

function [solu, info] = CG_CDP( z, A, y, ite_max, acu )

[n,L]=size(A);
l=norm(z)^2;
m=n*L;

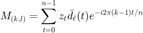计算信号 $z$ 的在衍射变换下的结果： $M_{(k,l)}=\displaystyle\sum_{t=0}^{n-1}z_t\bar{d}_\ell(t)e^{-i2\pi (k-1)t/n}$ 。注意到 MATLAB 函数 fft 对于矩阵输入，对其每一列计算一维的离散傅里叶变换。

rsd=fft(conj(A).*(z*ones(1,L)));

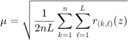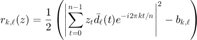计算 $\mu=\displaystyle\sqrt{\frac{1}{2nL}\sum_{k=1}^{n}\sum_{\ell=1}^L r_{(k,\ell)}(z)}$ 。注意到对于编码衍射模型， $r_{k,\ell}(z)=\displaystyle\frac{1}{2}\left( \left|\sum_{t=0}^{n-1}z_t\bar{d}_\ell(t)e^{-i2\pi kt/n} \right|^2 - b_{k,\ell} \right)$ 。

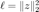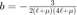$\ell=\|z\|_2^2$ , $a=\frac{1}{\ell+\mu}$ , $b=-\frac{3}{2(\ell+\mu)(4\ell+\mu)}$ 作为预条件中的两个参数。

mu=sqrt(sum(sum((abs(rsd).^2-y).^2))/2/m);
a=1/(l+mu);
b=-3/(2*(l+mu)*(4*l+mu));

由 Wirtinger 导数，有

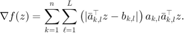
$\nabla f(z)=\displaystyle\sum_{k=1}^{n}\sum_{\ell=1}^L \left(|\bar{a}_{k,l}^\top z-b_{k,l}|\right)a_{k,l}\bar{a}_{k,l}^\top z.$

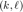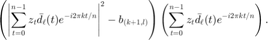
计算矩阵 t，其 $(k,\ell)$ 元素为 $\displaystyle\left(\left|\sum_{t=0}^{n-1}z_t\bar{d}_\ell(t)e^{-i2\pi kt/n}\right|^2-b_{(k+1,l)}\right)\left(\sum_{t=0}^{n-1}z_t\bar{d}_\ell(t)e^{-i2\pi kt/n} \right).$

t=(abs(rsd).^2-y).*rsd;

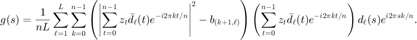
$g(s)=\displaystyle\frac{1}{nL}\sum_{\ell=1}^L\sum_{k=0}^{n-1} \left(\left|\sum_{t=0}^{n-1}z_t\bar{d}_\ell(t)e^{-i2\pi kt/n}\right|^2-b_{(k+1,\ell)} \right)\left(\sum_{t=0}^{n-1}z_t\bar{d}_\ell(t)e^{-i2\pi kt/n}\right) d_\ell(s)e^{i2\pi sk/n}.$

计算梯度 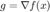$g=\nabla f(x)$ 。

g=mean(A.*ifft(t),2);

初始化。这里使用预优矩阵，计算$Mx^0=g^0$，其中 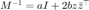$M^{-1}=aI+2bz\bar{z}^\top$ 。

xk=a*g+b*(2*real(z'*g))*z;

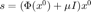$s=(\Phi(x^0)+\mu I)x^0$ ，这里的推导和下文迭代主循环中一致，省略。

t1=abs(rsd).^2.*fft(conj(A).*(xk*ones(1,L)));
t2=n*rsd.^2.*ifft(A.*(conj(xk)*ones(1,L)));
s1=mean(A.*ifft(t1),2);
s2=mean(A.*ifft(t2),2);
s=s1+s2+mu*xk;

残差的初始化：$r^0=g^0-(\Phi(x^0)+\mu I)x^0$。

rk=g-s;

在 acu 为1的情况下采用更精确的 LM 方法，取 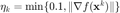$\eta_k=\min \{0.1,\|\nabla f(\mathbf{x}^k)\|\}$ ; 否则，采取 $\eta_k=0.1$ 。

if acu == 1
    cri = min(0.1,min(0.1*norm(g),norm(g)^2));
else
    cri = min(0.1,0.1*norm(g));
end

迭代次数记为 0。以 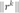$\|r^k\|$ 为收敛判断依据。

K=0;
C=norm(rk);

迭代循环

当 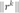$\|r^k\|$ 小于阈值或者迭代次数超过限制时，停止迭代。

while K<ite_max && C>cri

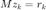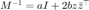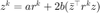从预条件方程中解得 $z_k$ ，有 $M z_k=r_k$ 。这里我们取 $M^{-1}=aI+2bz\bar{z}^\top$ ，可以推出 $z^{k}=ar^k+2b(\bar{z}^\top r^kz)$ 。注意到这里的 $z$ 不是迭代变量，而是迭代的初始值。

    zk=a*rk+b*(2*real(z'*rk))*z;
    K=K+1;

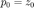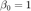初次迭代，取 $p_0=z_0$ , $\beta_0=1$ 。

    if K==1
        pk=zk;
        rho=2*real(rk'*zk);
    else

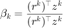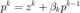令 $\displaystyle\beta_{k}=\frac{(r^{k})^\top z^{k}}{(r^{k})^\top z^{k}}$ , $\displaystyle p^{k}=z^{k}+\beta_{k} p^{k-1}$ 。

        rho1=rho;
        rho=2*real(rk'*zk);
        beta=rho/rho1;
        pk=zk+beta*pk;
    end

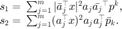
$\begin{array}{rl} s_1=&\hspace{-0.5em}\sum_{j=1}^m |\bar{a}_j^\top x|^2 a_j\bar{a_j}^\top p^k,\\ s_2=&\hspace{-0.5em}\sum_{j=1}^m (a_j^\top x)^2a_ja_j^\top \bar{p}_k. \end{array}$

    t1=abs(rsd).^2.*fft(conj(A).*(pk*ones(1,L)));
    s1=mean(A.*ifft(t1),2);
    t2=n*rsd.^2.*ifft(A.*(conj(pk)*ones(1,L)));
    s2=mean(A.*ifft(t2),2);

计算高斯-牛顿矩阵

$\Phi(\mathbf{x})=\overline{J(\mathbf{x})}^\top J(\mathbf{x})= \sum_{j=1}^m\left[ \begin{array}{ll}|\bar{a}_j^\top x|^2a_j\bar{a}_j^\top & (\bar{a}_j^\top x)^2a_ja_j^\top\\ (\overline{\bar{a}_j^\top x})^2\bar{a}_j\bar{a}_j^\top & |\bar{a}_j^\top x|^2\bar{a}_ja_j^\top\end{array} \right] = \left[ \begin{array}{ll} \Phi_{11} & \Phi_{12} \\ \bar{\Phi}_{12} & \bar{\Phi_{11}} \end{array} \right].$

考虑到共轭，我们只取上半部分，令 $\Psi(x)=\left[ \Phi_{11} \Phi_{12} \right]$ , $\mathbf{p}=\left[\begin{array}{l} p\\\bar{p} \end{array}\right]$ ，则有 $(\Psi(x)+\mu [I,0])\mathbf{p}=s_1+s_2+\mu p$ 。

预条件共轭梯度法的步长 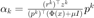$\alpha_k=\frac{(r^k)^\top z^k}{(p^k)^\top (\Phi(x)+\mu I)}p^k$ 。

    s=s1+s2+mu*pk;
    alpha=rho/(2*real(pk'*s));

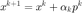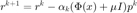共轭梯度法的迭代步， $\displaystyle x^{k+1}=x^k+\alpha_k p^k$ , $\displaystyle r^{k+1}=r^k-\alpha_k (\Phi(x)+\mu I)p^k$ 。

    xk=xk+alpha*pk;
    rk=rk-alpha*s;
    % 以 $r^k$ 的模长作为停机判断依据。
    C=norm(rk);
end

退出迭代时，记录当前迭代步、矩阵向量积次数。返回 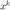$x^k$ 为解。

info.ite=K;
info.prod=6+4*info.ite;
solu=xk;

end

参考页面

此页面被编码衍射模型的 LM 算法调用。

此页面的源代码请见： CG_CDP.m。

版权声明

此页面为《最优化：建模、算法与理论》、《最优化计算方法》配套代码。代码作者：文再文、刘浩洋、户将，代码整理与页面制作：杨昊桐。

编码衍射模型 LM 子问题的预条件（截断）共轭梯度算法

目录

初始化和迭代准备

迭代循环

参考页面

版权声明