实例:利用增广拉格朗日函数法解基追踪问题
考虑基追踪问题:
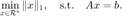
这里使用内层循环为近似点梯度法的增广拉格朗日函数法对其进行求解。 引入罚因子  和乘子
和乘子  ,则增广拉格朗日函数为
,则增广拉格朗日函数为
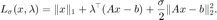
对  和
和  进行迭代。
进行迭代。
目录
构造基追踪问题
设定随机种子。
clear; seed = 97006855; ss = RandStream('mt19937ar','Seed',seed); RandStream.setGlobalStream(ss);
构造基追踪问题,  为问题的真实解(其稀疏度为
为问题的真实解(其稀疏度为 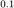 ),使得
),使得 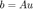 ,
,  为随机的迭代初始点。
为随机的迭代初始点。
m = 512; n = 1024; A = randn(m, n); u = sprandn(n, 1, 0.1); b = A * u; x0 = randn(n, 1);
参数设定。
opts.verbose = 0; opts.gamma = 0.85; opts.itr = 7;
求解基追踪问题
调用算法 BP_ALM 求解 BP 问题。
[x, out] = BP_ALM(x0, A, b, opts); k1 = out.itr + 1;
记录等式约束的违反度。
data1 = out.feavec(1:k1);
计算并存储迭代点距离最优点的距离。
tmp = [x0,out.itervec(:,1:k1-1)] - u*ones(1,k1); tmp2 = sum(tmp.*tmp); data2 = sqrt(tmp2);
取稀疏度 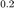 重复实验。
重复实验。
seed = 97006855; ss = RandStream('mt19937ar','Seed',seed); RandStream.setGlobalStream(ss); m = 512; n = 1024; A = randn(m, n); u = sprandn(n, 1, 0.2); b = A * u; x0 = randn(n, 1); [x, out] = BP_ALM(x0, A, b, opts); k2 = out.itr + 1; data3 = out.feavec(1:k2); tmp = [x0,out.itervec(:,1:k2-1)] - u*ones(1,k2); tmp2 = sum(tmp.*tmp); data4 = sqrt(tmp2);
结果可视化
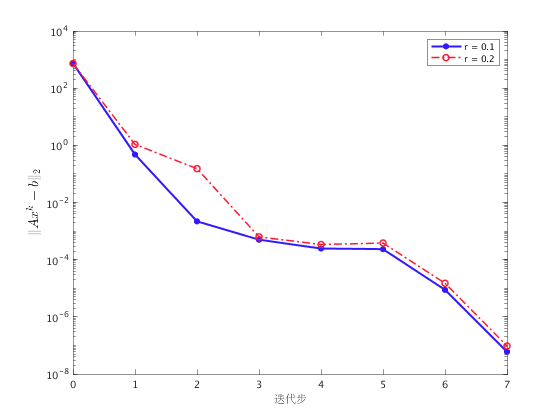
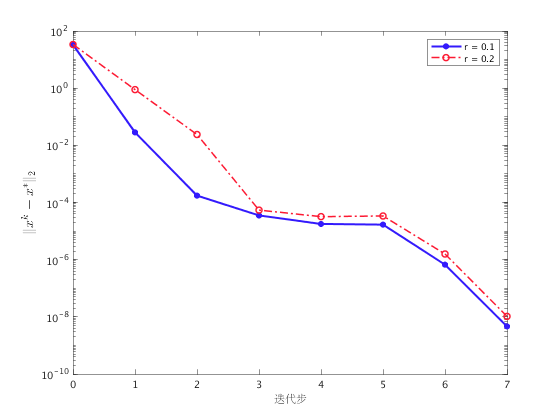
分别展示约束违反度和距离真实解的距离随着迭代步的变化。
fig = figure; semilogy(0:k1-1, data1, '-*', 'Color',[0.2 0.1 0.99], 'LineWidth',2); hold on semilogy(0:k2-1, data3, '-.o','Color',[0.99 0.1 0.2], 'LineWidth',1.5); legend('r = 0.1' ,'r = 0.2'); ylabel('$\|Ax^k - b\|_2$', 'fontsize', 14, 'interpreter', 'latex'); xlabel('迭代步'); print(fig, '-depsc','iter-alm.eps'); fig = figure; semilogy(0:k1-1, data2, '-*', 'Color',[0.2 0.1 0.99], 'LineWidth',2); hold on semilogy(0:k2-1, data4, '-.o','Color',[0.99 0.1 0.2], 'LineWidth',1.5); legend('r = 0.1' ,'r = 0.2'); ylabel('$\|x^k - x^*\|_2$', 'fontsize', 14, 'interpreter', 'latex'); xlabel('迭代步'); print(fig, '-depsc','fea-alm.eps');
结果分析
对于基追踪问题,取固定的非负拉格朗日罚因子,可以保证其收敛性。上图展示了在固定罚因子  的情况下不同稀疏度
的情况下不同稀疏度  的收敛情况,分别表示约束违反度
的收敛情况,分别表示约束违反度 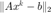 、当前点与最优点的距离
、当前点与最优点的距离 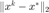 随迭代的变化。 我们观察到两次实验中,增广拉格朗日函数法均达到收敛。
随迭代的变化。 我们观察到两次实验中,增广拉格朗日函数法均达到收敛。
参考页面
模型利用内层循环为近似点梯度法的增广拉格朗日函数算法求解,算法见 基追踪问题的增广拉格朗日函数法解法。
此页面的源代码请见: demo_alm.m。
版权声明
此页面为《最优化:建模、算法与理论》、《最优化计算方法》配套代码。 代码作者:文再文、刘浩洋、户将,代码整理与页面制作:杨昊桐。
著作权所有 (C) 2020 文再文、刘浩洋、户将