截断共轭梯度法
考虑信赖域子问题: 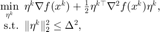 其中
其中 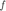 是目标函数,$\nabla f(x), \nabla^2 f(x)$ 表示
是目标函数,$\nabla f(x), \nabla^2 f(x)$ 表示 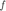 的梯度与海瑟矩阵。注意,当
的梯度与海瑟矩阵。注意,当  时,信赖域子问题就等同于求解牛顿方程。
时,信赖域子问题就等同于求解牛顿方程。
这里,实现截断共轭梯度法 (Steihaug-Toint Conjugate gradient, ST-CG 方法)来求解上述信赖域子问题。
当约束不存在时(即  ),共轭梯度法通过求解一系列共轭方向可以快速求解对应的无约束二次优化问题。具体地,对于问题
),共轭梯度法通过求解一系列共轭方向可以快速求解对应的无约束二次优化问题。具体地,对于问题 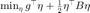 ,给定初始
,给定初始 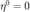 ,
, 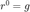 ,
, 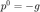 ,共轭梯度法的迭代格式为:
,共轭梯度法的迭代格式为:
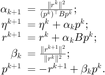
当信赖域约束存在时,共轭梯度法得到的解不能保证落在可行域内。因此,截断共轭梯度法则在共轭梯度法增加两条额外的终止条件,用于处理负曲率 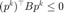 或超过信赖域半径
或超过信赖域半径 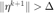 的情况。
的情况。
目录
初始化和迭代准备
输入信息:迭代点  ,梯度 grad,海瑟矩阵 hess,信赖域半径
,梯度 grad,海瑟矩阵 hess,信赖域半径  , 包含算法参数的结构体 opts 。 输出信息:信赖域子问题的解
, 包含算法参数的结构体 opts 。 输出信息:信赖域子问题的解  (也就是迭代点
(也就是迭代点  处的下降方向), Heta 为海瑟矩阵在点
处的下降方向), Heta 为海瑟矩阵在点  作用在方向
作用在方向  上的结果,即
上的结果,即 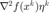 ,记录迭代信息的结构体 out 和记录退出原因的标记 stop_tCG 。
,记录迭代信息的结构体 out 和记录退出原因的标记 stop_tCG 。
function [eta, Heta, out, stop_tCG] ... = tCG(x, grad, hess, Delta, opts)
从输入的结构体 opts 中读取参数或采取默认参数。
- opts.kappa:牛顿方程求解精度的参数
- theta:牛顿方程求精精度的参数
- opts.maxit:最大迭代次数,对于共轭梯度法而言默认等于变量的维度
- opts.minit:最小迭代次数
if ~isfield(opts,'kappa'); opts.kappa = 0.1; end if ~isfield(opts,'theta'); opts.theta = 1; end if ~isfield(opts,'maxit'); opts.maxit = length(x); end if ~isfield(opts,'minit'); opts.minit = 5; end % 参数复制。 theta = opts.theta; kappa = opts.kappa;
初始化,  为优化变量,初始为全 0向量:$\mathbf{0}$。
为优化变量,初始为全 0向量:$\mathbf{0}$。  初始化为目标函数的梯度
初始化为目标函数的梯度 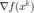 。
。
eta = zeros(size(x)); Heta = eta; r = grad; e_Pe = 0; r_r = r'*r; norm_r = sqrt(r_r); norm_r0 = norm_r;
共轭梯度法初始时刻的共轭方向 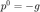 并在代码中以 mdelta 表示
并在代码中以 mdelta 表示 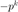 (minus delta)。
(minus delta)。
mdelta = r; d_Pd = r_r; e_Pd = 0;
共轭梯度法优化的目标函数。
model_fun = @(eta, Heta) eta'*grad + .5*(eta'*Heta); model_value = 0;
当迭代以达到最大迭代步数停止时,记 stop_tCG=5。
stop_tCG = 5;
迭代主循环
最大迭代步数为 maxit
for j = 1 : opts.maxit
 表示梯度,
表示梯度, 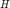 表示海瑟矩阵。此处计算
表示海瑟矩阵。此处计算 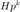 。注意到这一步计算的耗时相对较长。
。注意到这一步计算的耗时相对较长。
Hmdelta = hess(mdelta);
计算曲率 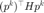 和共轭梯度法的步长
和共轭梯度法的步长 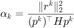 。
。
在当前的搜索方向和步长下,我构造新的共轭方向 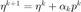 。计算
。计算 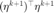 ,以便进行截断共轭梯度法的检查。为了简化计算这里利用了
,以便进行截断共轭梯度法的检查。为了简化计算这里利用了 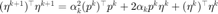 。
。
d_Hd = mdelta'*Hmdelta;
alpha = r_r/d_Hd;
e_Pe_new = e_Pe + 2.0*alpha*e_Pd + alpha*alpha*d_Pd;
截断共轭梯度法需要对曲率进行检查,如果曲率满足 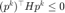 , 说明海瑟矩阵不正定(再求解下去得到的方向不一定是下降方向),则停止共轭梯度算法。当
, 说明海瑟矩阵不正定(再求解下去得到的方向不一定是下降方向),则停止共轭梯度算法。当 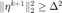 时, 迭代点超出可行域边界,则通过构造得到一个位于边界上的近似解并停止算法。
时, 迭代点超出可行域边界,则通过构造得到一个位于边界上的近似解并停止算法。
当上述两条件中的任何一个成立,计算  使得
使得 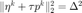 。 以
。 以 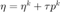 为最终的迭代结果。更新
为最终的迭代结果。更新 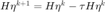 。
。
if d_Hd <= 0 || e_Pe_new >= Delta^2
tau = (-e_Pd + sqrt(e_Pd*e_Pd + d_Pd*(Delta^2-e_Pe))) / d_Pd;
eta = eta - tau*mdelta;
Heta = Heta -tau*Hmdelta;
记录共轭梯度法的退出条件,当以非正曲率退出时记为 1,以超出边界退出时记为 2。退出迭代。
if d_Hd <= 0 stop_tCG = 1; else stop_tCG = 2; end break; end
如果一步迭代更新的 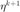 没有达到截断共轭梯度法的两个新增的停止条件,则更新
没有达到截断共轭梯度法的两个新增的停止条件,则更新 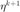 。
。
e_Pe = e_Pe_new;
new_eta = eta-alpha*mdelta;
new_Heta = Heta -alpha*Hmdelta;
计算 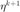 处的目标函数值。如果一步更新后的目标函数值没有下降,退出迭代,拒绝该步更新。 stop_tCG==6 表示目标函数值非降而终止。
处的目标函数值。如果一步更新后的目标函数值没有下降,退出迭代,拒绝该步更新。 stop_tCG==6 表示目标函数值非降而终止。
new_model_value = model_fun(new_eta, new_Heta);
if new_model_value >= model_value
stop_tCG = 6;
break;
end
如果没有达到上述两种情况,接受更新的 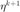 ,利用新的
,利用新的 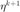 更新变量。
更新变量。
eta = new_eta;
Heta = new_Heta;
model_value = new_model_value;
更新残差 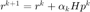 以及其范数。特别的,记录上一步的
以及其范数。特别的,记录上一步的 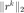 为 r_rold。
为 r_rold。
r = r -alpha*Hmdelta;
r_rold = r_r;
r_r = r'*r;
norm_r = sqrt(r_r);
标准的共轭梯度法的收敛条件:当达到最小迭代次数,且 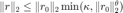 时,认为算法收敛,停止迭代。
时,认为算法收敛,停止迭代。
满足上述收敛条件时,如果 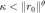 ,则说明条件
,则说明条件 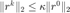 为更严格的条件,说明此时外层牛顿法或者信赖域方法处于线性收敛的阶段。 反之,条件
为更严格的条件,说明此时外层牛顿法或者信赖域方法处于线性收敛的阶段。 反之,条件 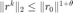 更严格,说明此时
更严格,说明此时 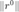 已经较小,此时对应外层牛顿法或者信赖域方法的超线性收敛阶段。
已经较小,此时对应外层牛顿法或者信赖域方法的超线性收敛阶段。
if j >= opts.minit && norm_r <= norm_r0*min(norm_r0^theta, kappa) if kappa < norm_r0^theta stop_tCG = 3; else stop_tCG = 4; end break; end
计算新的搜索方向: 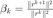 ,
, 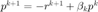 。
。
beta = r_r/r_rold;
mdelta = r + beta*mdelta;
更新 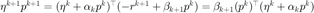 ,这是由于
,这是由于 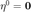 且
且 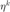 为
为  的线性组合,则由
的线性组合,则由 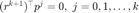 可知
可知 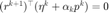 。
。
以及 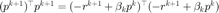 ,注意到
,注意到 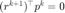 ,有
,有 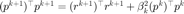 。
。
e_Pd = beta*(e_Pd + alpha*d_Pd);
d_Pd = r_r + beta*beta*d_Pd;
end
退出循环,记录退出信息。
out.iter = j; out.stop_tCG = stop_tCG;
end
参考页面
此页面实现了截断共轭梯度算法,该函数用于 非精确牛顿法 中的牛顿方程的近似求解以及 信赖域方法 中的信赖域子问题的求解。
此页面的源代码请见: tCG.m。
版权声明
此页面为《最优化:建模、算法与理论》、《最优化计算方法》配套代码。 代码作者:文再文、刘浩洋、户将,代码整理与页面制作:杨昊桐。
著作权所有 (C) 2020 文再文、刘浩洋、户将