信赖域方法解优化问题
考虑无约束光滑优化问题:
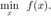
在第  步迭代,信赖域方法对目标函数
步迭代,信赖域方法对目标函数 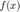 在
在  附近用如下二次函数逼近:
附近用如下二次函数逼近: 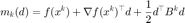 , 其中
, 其中 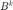 是一个对称矩阵,可以是精确海瑟矩阵或者海瑟矩阵的近似。 同时,令
是一个对称矩阵,可以是精确海瑟矩阵或者海瑟矩阵的近似。 同时,令 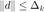 限制区域大小以保证该二次函数的逼近质量。结合两者,信赖域子问题可以写为:
限制区域大小以保证该二次函数的逼近质量。结合两者,信赖域子问题可以写为:
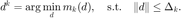
在得到 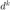 之后,计算
之后,计算 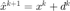 和比值
和比值 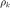 :
: 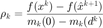 来确定是否更新当前迭代。如果
来确定是否更新当前迭代。如果 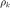 较大,我们认为
较大,我们认为 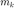 在
在 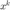 附近逼近
附近逼近 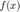 的质量较好,更新
的质量较好,更新 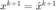 , 并增大信赖域半径
, 并增大信赖域半径 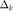 (如乘以一个大于1的常数)。否则,则拒绝更新,即令
(如乘以一个大于1的常数)。否则,则拒绝更新,即令 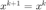 ,并减小
,并减小 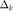 (如乘以一个小于1的数)。
(如乘以一个小于1的数)。
这里,对于信赖域子问题的求解,我们采用截断共轭梯度法,见 截断共轭梯度法。
目录
初始化和迭代准备
输入信息:初始迭代点 x ,目标函数值和梯度计算函数 fun ,海瑟矩阵 hess 以及算法求解相关参数的结构体 opts 。
输出信息:迭代得到的解 x 和迭代信息结构体 out 。
- out.msg :标记停机时算法的求解状态
- out.nrmG :记录迭代过程的梯度范数
- out.nrmg :记录迭代退出时的梯度范数
- out.iter :记录迭代退出时的迭代步数
- out.f :记录迭代退出时的函数值
- out.nfe :调用原函数的次数
function [x, out] = fminTR(x,fun, hess, opts, varargin)
检查输入信息,MATLAB 以 nargin 表示函数输入的参数个数。当参数量不足 3 时报错, 等于 3 时认为 opts 为空结构体,即全部采用默认参数。
从输入的结构体中读取参数或采取默认参数。
- opts.ftol :针对函数值的停机准则
- opts.gtol :针对梯度范数的停机准则
- opts.eta1 :
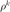 的下界(当超出此界时意味着信赖域半径需要缩小并拒绝更新)
的下界(当超出此界时意味着信赖域半径需要缩小并拒绝更新) - opts.eta2 :
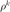 的上界(当超出此界时意味着信赖域半径需要增大并接受更新)
的上界(当超出此界时意味着信赖域半径需要增大并接受更新) - opts.gamma1 :每次调整信赖域半径缩小的比例
- opts.gamma2 :每次调整信赖域半径增大的比例
- opts.maxit :主循环的最大迭代次数
- opts.record :是否需要打印迭代信息
- opts.verbose :是否需要打印半径调整信息
- opts.itPrint :每隔几步输出一次迭代信息
if (nargin < 3); error('[x, out] = fminTR(fun, x, opts)'); end if (nargin < 4); opts = []; end if ~isfield(opts,'gtol'); opts.gtol = 1e-6; end if ~isfield(opts,'ftol'); opts.ftol = 1e-12; end if ~isfield(opts,'eta1'); opts.eta1 = 1e-2; end if ~isfield(opts,'eta2'); opts.eta2 = 0.9; end if ~isfield(opts,'gamma1'); opts.gamma1 = .25; end if ~isfield(opts,'gamma2'); opts.gamma2 = 10; end if ~isfield(opts,'maxit'); opts.maxit = 200; end if ~isfield(opts,'record'); opts.record = 0; end if ~isfield(opts,'itPrint'); opts.itPrint = 1; end if ~isfield(opts,'verbose'); opts.verbose = 0; end
从结构体中复制参数。
maxit = opts.maxit; record = opts.record; itPrint = opts.itPrint; gtol = opts.gtol; ftol = opts.ftol; eta1 = opts.eta1; eta2 = opts.eta2; gamma1 = opts.gamma1; gamma2 = opts.gamma2;
迭代准备,计算初始点  处的函数值和梯度。
处的函数值和梯度。
out = struct(); [f,g] = fun(x); out.nfe = 1; nrmg = norm(g,2); out.nrmG = nrmg; fp = f; gp = g;
信赖域子问题利用截断共轭梯度法求解,利用结构体 opts_tCG 为其提供参数。
opts_tCG = struct();
初始化信赖域半径。初始值设定为提供的参数值或默认值 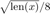 并令
并令  的上界
的上界  为
为  。
。
Delta_bar = sqrt(length(x)); Delta0 = Delta_bar/8; if isfield(opts,'Delta') Delta = opts.Delta; else Delta = Delta0; end
两个参数分别记录信赖域半径连续增大或减小的次数,以方便初始值的调整。
consecutive_TRplus = 0; consecutive_TRminus = 0;
将 tCG.m 存放的目录加入工作目录。
addpath('../newton');
当需要详细输出时,设定输出格式。
if record >= 1 if ispc; str1 = ' %10s'; str2 = ' %8s'; else str1 = ' %10s'; str2 = ' %8s'; end stra = ['%5s', str1, str2, str2, str2, str2, str2, str2, '\n']; str_head = sprintf(stra, ... 'iter', 'F', 'fdiff', 'mdiff', 'redf', 'ratio', 'Delta', 'nrmg'); fprintf('%s', str_head); str_num = ['%4d %+8.7e %+2.1e %+2.1e %+2.1e %+2.1e %2.1e %2.1e']; end
迭代主循环
以 maxit 为最大迭代次数。
for iter = 1:maxit
截断共轭梯度法中用于判断收敛的参数。
opts_tCG.kappa = 0.1;
opts_tCG.theta = 1;
调用 tCG 函数,利用截断共轭梯度法求解信赖域子问题,得到迭代方向  。 stop_tCG 表示截断共轭梯度法的退出原因。
。 stop_tCG 表示截断共轭梯度法的退出原因。
hess_tCG = @(d) hess(x,d);
[d, Hd, out_tCG] = tCG(x, gp, hess_tCG, Delta, opts_tCG);
stop_tCG = out_tCG.stop_tCG;
计算比值
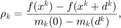
以确定是否更新迭代和修正信赖域半径。 首先计算 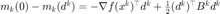 ,为了保证数值稳定性,增加一个小常数 rreg 。
,为了保证数值稳定性,增加一个小常数 rreg 。
mdiff = g'*d + .5*d'*Hd;
rreg = 10*max(1, abs(fp)) * eps;
mdiff = -mdiff + rreg;
model_decreased = mdiff > 0;
构造试验点 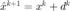 ,并计算该点处计算函数值和梯度。
,并计算该点处计算函数值和梯度。
xnew = x + d;
[f,g] = fun(xnew);
nrmg = norm(g,2);
out.nfe = out.nfe + 1;
计算 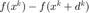 ,同样地增加一个小常数 rreg。 然后计算
,同样地增加一个小常数 rreg。 然后计算 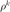 作为修正信赖域半径和判断是否更新的依据。
作为修正信赖域半径和判断是否更新的依据。
redf = fp - f + rreg;
ratio = redf/mdiff;
当 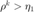 时,接受此次更新,并记录上一步的函数值和梯度。
时,接受此次更新,并记录上一步的函数值和梯度。
if ratio >= eta1 x = xnew; fp = f; gp = g; out.nrmG = [out.nrmG; nrmg]; end
计算函数值相对变化。
fdiff = abs(redf/(abs(fp)+1));
停机准则:当满足(1)梯度范数小于阈值或(2)函数值的相对变化小于阈值且 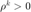 时,停止迭代。
时,停止迭代。
cstop = nrmg <= gtol || (abs(fdiff) <= ftol && ratio > 0);
% 当需要详细输出时,在(1)开始迭代时(2)达到收敛时(3)达到最大迭代次数退出迭代时
% (4)每若干步时,打印详细结果。
if record>=1 && (cstop || ...
iter == 1 || iter==maxit || mod(iter,itPrint)==0)
if mod(iter,20*itPrint) == 0 && iter ~= maxit && ~cstop
fprintf('\n%s', str_head);
end
stop_tCG 记录内层的截断共轭梯度法退出的原因,分别对应输出如下:
switch stop_tCG case{1} str_tCG = ' [negative curvature]\n'; case{2} str_tCG = ' [exceeded trust region]\n'; case{3} str_tCG = ' [linear convergence]\n'; case{4} str_tCG = ' [superlinear convergence]\n'; case{5} str_tCG = ' [maximal iteration number reached]\n'; case{6} str_tCG = ' [model did not decrease]\n'; end fprintf(strcat(str_num,str_tCG), ... iter, f, fdiff, mdiff, redf, ratio, Delta, nrmg); end
当满足停机准则时,记录达到最优值,退出循环。
if cstop out.msg = 'optimal'; break; end
信赖域半径的调整
如果 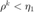 或者算法非降(或者当
或者算法非降(或者当 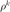 计算时出现分母约为 0 ,即
计算时出现分母约为 0 ,即 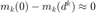 )时,不接受当前步迭代。这种情况下,需要对信赖域半径进行缩减。
)时,不接受当前步迭代。这种情况下,需要对信赖域半径进行缩减。
具体而言,令 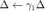 ,将信赖域半径的连续增大次数置零, 缩小次数加一。
,将信赖域半径的连续增大次数置零, 缩小次数加一。
if ratio < eta1 || ~model_decreased || isnan(ratio)
Delta = Delta*gamma1;
consecutive_TRplus = 0;
consecutive_TRminus = consecutive_TRminus + 1;
当信赖域半径连续 5 次减小时,认为当前的信赖域半径过大,并输出相应的提示信息。
if consecutive_TRminus >= 5 && opts.verbose >= 1 consecutive_TRminus = -inf; fprintf(' +++ Detected many consecutive TR- (radius decreases).\n'); fprintf(' +++ Consider decreasing options.Delta_bar by an order of magnitude.\n'); fprintf(' +++ Current values: options.Delta_bar = %g and options.Delta0 = %g.\n', options.Delta_bar, options.Delta0); end
当 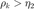 且
且 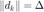 (对应为截断共轭梯度法因遇到负曲率或者超出信赖域半径而终止), 增大信赖域半径。
(对应为截断共轭梯度法因遇到负曲率或者超出信赖域半径而终止), 增大信赖域半径。 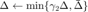 (
(  为信赖域半径的上界,设置为
为信赖域半径的上界,设置为  )。 将信赖域半径的连续减小次数置零,增大次数加一。
)。 将信赖域半径的连续减小次数置零,增大次数加一。
elseif ratio > eta2 && (stop_tCG == 1 || stop_tCG == 2)
Delta = min(gamma2*Delta, Delta_bar);
consecutive_TRminus = 0;
consecutive_TRplus = consecutive_TRplus + 1;
考虑当信赖域半径连续 5 次增大时,认为当前的信赖域半径过小,输出相应的提示信息。
if consecutive_TRplus >= 5 && opts.verbose >= 1 consecutive_TRplus = -inf; fprintf(' +++ Detected many consecutive TR+ (radius increases).\n'); fprintf(' +++ Consider increasing options.Delta_bar by an order of magnitude.\n'); fprintf(' +++ Current values: options.Delta_bar = %g and options.Delta0 = %g.\n', Delta_bar, Delta0); end
除了以上两种情况,不需要对信赖域半径进行调整,将其连续增大和减小次数都置零。
else consecutive_TRplus = 0; consecutive_TRminus = 0; end
end
当从外层迭代退出时,记录退出信息。
out.iter = iter; out.f = f; out.nrmg = nrmg;
end
参考页面
我们在页面 实例:信赖域算法解逻辑回归问题 中展示了该算法的一个应用。另外,该算法调用截断共轭梯度法 tCG 求解信赖域子问题,关于截断共轭梯度法参考 截断共轭梯度法。
此页面的源代码请见: fminTR.m。
版权声明
此页面为《最优化:建模、算法与理论》、《最优化计算方法》配套代码。 代码作者:文再文、刘浩洋、户将,代码整理与页面制作:杨昊桐。
著作权所有 (C) 2020 文再文、刘浩洋、户将