实例：利用信赖域方法求解逻辑回归问题

考虑逻辑回归问题

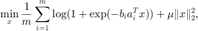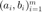$\displaystyle \min_x \frac{1}{m}\sum_{i=1}^m \log(1+ \exp(-b_ia_i^Tx)) + \mu\|x\|_2^2,$ 其中 $(a_i,b_i)_{i=1}^m$ 为已知的待分类的数据集。这里利用信赖域方法求解该问题（使用截断共轭梯度法求解信赖域子问题）。

该优化问题目标函数的梯度和海瑟矩阵：

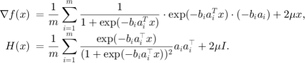
$\begin{array}{rl} \nabla f(x) &\hspace{-0.5em}\displaystyle= \frac{1}{m}\sum_{i=1}^m \frac{1}{1+\exp(-b_ia_i^Tx)} \cdot \exp(-b_ia_i^Tx) \cdot (-b_ia_i) + 2\mu x, \\ H(x)&\hspace{-0.5em}\displaystyle= \frac{1}{m}\sum_{i=1}^m \frac{\exp(-b_ia_i^\top x)}{(1+\exp(-b_ia_i^\top x))^2}a_ia_i^\top + 2\mu I. \end{array}$

逻辑回归问题

在不同的数据集上进行实验。导入 LIBSVM 数据集 a9a 上的实验，|libsvmread| 为另外运行的读入程序。

dataset = 'a9a.test';
[b,A] = libsvmread(dataset);
[m,n] = size(A);
mu = 1e-2/m;

设定参数。

opts = struct();
opts.xtol = 1e-8;
opts.gtol = 1e-6;
opts.ftol = 1e-16;
opts.record  = 1;
opts.verbose = 1;
opts.Delta = sqrt(n);
fun = @(x) lr_loss(A,b,m,x,mu);
x0 = zeros(n,1);
hess = @(x,u) hess_lr(A,b,m,mu,x,u);

调用信赖域方法求解。

[x1,out1] = fminTR(x0,fun,hess,opts);

在 CINA 数据集上的实验。

dataset = 'CINA.test';
[b,A] = libsvmread(dataset);
Atran = A';
[m,n] = size(A);
fun = @(x) lr_loss(A,b,m,x,mu);
x0 = zeros(n,1);
hess = @(x,u) hess_lr(A,b,m,mu,x,u);
[x2,out2] = fminTR(x0,fun,hess,opts);

在 ijcnn1 数据集上的实验。

dataset = 'ijcnn1.test';
[b,A] = libsvmread(dataset);
Atran = A';
[m,n] = size(A);
mu = 1e-2/m;
fun = @(x) lr_loss(A,b,m,x,mu);
x0 = zeros(n,1);
hess = @(x,u) hess_lr(A,b,m,mu,x,u);
[x3,out3] = fminTR(x0,fun,hess,opts);

结果可视化

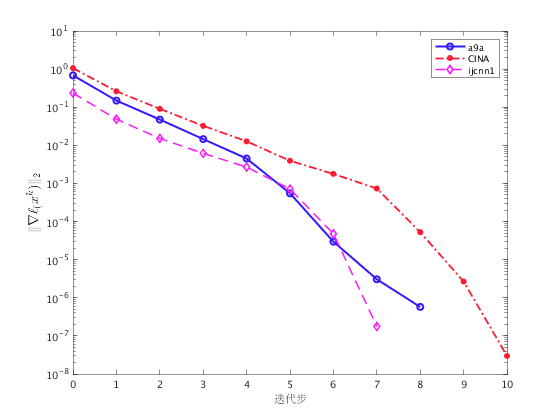
将目标函数梯度范数随着迭代步的变化信息可视化

fig = figure;
semilogy(0:out1.iter, out1.nrmG, '-o', 'Color',[0.2 0.1 0.99], 'LineWidth',2);
hold on
semilogy(0:out2.iter, out2.nrmG, '-.*', 'Color',[0.99 0.1 0.2], 'LineWidth',1.8);
hold on
semilogy(0:out3.iter, out3.nrmG, '--d', 'Color',[0.99 0.1 0.99], 'LineWidth',1.5);
legend('a9a','CINA','ijcnn1');
ylabel('$\|\nabla \ell_(x^k)\|_2$', 'fontsize', 14, 'interpreter', 'latex');
xlabel('迭代步');
print(fig, '-depsc','lr_tr.eps');

辅助函数

逻辑回归问题的目标函数

function [f,g] = lr_loss(A,b,m,x,mu)
Ax = A*x;
Atran = A';
expba = exp(- b.*Ax);
f = sum(log(1 + expba))/m + mu*norm(x,2)^2;
if nargout > 1
   g = Atran*(b./(1+expba) - b)/m + 2*mu*x;
end
end

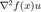目标函数的海瑟矩阵，函数要求提供当前自变量 $x$ 和向量 $u$ ，实际返回海瑟矩阵和向量 $u$ 的乘积 $\nabla^2 f(x)u$ 。

function H = hess_lr(A,b,m,mu,x,u)
    Ax = A*x;
    Atran = A';
    expba = exp(- b.*Ax);
    p = 1./(1 + expba);
    w = p.*(1-p);
    H = Atran*(w.*(A*u))/m + 2*mu*u;
end

 iter           F     fdiff     mdiff      redf     ratio     Delta      nrmg
   1  +3.8222757e-01  +2.2e-01  +2.7e-01  +3.1e-01  +1.1e+00  1.1e+01  1.5e-01 [linear convergence]
   2  +3.3668757e-01  +3.4e-02  +3.7e-02  +4.6e-02  +1.2e+00  1.1e+01  4.7e-02 [linear convergence]
   3  +3.2377263e-01  +9.8e-03  +1.1e-02  +1.3e-02  +1.2e+00  1.1e+01  1.5e-02 [superlinear convergence]
   4  +3.1925140e-01  +3.4e-03  +4.1e-03  +4.5e-03  +1.1e+00  1.1e+01  4.5e-03 [superlinear convergence]
   5  +3.1881829e-01  +3.3e-04  +4.0e-04  +4.3e-04  +1.1e+00  1.1e+01  5.5e-04 [superlinear convergence]
   6  +3.1879833e-01  +1.5e-05  +1.8e-05  +2.0e-05  +1.1e+00  1.1e+01  3.0e-05 [maximal iteration number reached]
   7  +3.1879713e-01  +9.1e-07  +1.1e-06  +1.2e-06  +1.1e+00  1.1e+01  3.1e-06 [maximal iteration number reached]
   8  +3.1879712e-01  +1.1e-08  +1.4e-08  +1.4e-08  +1.0e+00  1.1e+01  5.8e-07 [maximal iteration number reached]
 iter           F     fdiff     mdiff      redf     ratio     Delta      nrmg
   1  +2.8353140e-01  +3.2e-01  +3.6e-01  +4.1e-01  +1.1e+00  1.1e+01  2.6e-01 [linear convergence]
   2  +2.1686206e-01  +5.5e-02  +5.3e-02  +6.7e-02  +1.3e+00  1.1e+01  9.1e-02 [linear convergence]
   3  +1.8970171e-01  +2.3e-02  +2.2e-02  +2.7e-02  +1.2e+00  1.1e+01  3.2e-02 [superlinear convergence]
   4  +1.6887294e-01  +1.8e-02  +1.7e-02  +2.1e-02  +1.2e+00  1.1e+01  1.3e-02 [superlinear convergence]
   5  +1.6066740e-01  +7.1e-03  +6.6e-03  +8.2e-03  +1.2e+00  1.1e+01  3.9e-03 [exceeded trust region]
   6  +1.5747024e-01  +2.8e-03  +2.9e-03  +3.2e-03  +1.1e+00  1.1e+01  1.8e-03 [exceeded trust region]
   7  +1.5567260e-01  +1.6e-03  +1.7e-03  +1.8e-03  +1.1e+00  1.1e+01  7.3e-04 [exceeded trust region]
   8  +1.5555589e-01  +1.0e-04  +1.1e-04  +1.2e-04  +1.1e+00  1.1e+01  5.3e-05 [maximal iteration number reached]
   9  +1.5555406e-01  +1.6e-06  +1.8e-06  +1.8e-06  +1.0e+00  1.1e+01  2.7e-06 [maximal iteration number reached]
  10  +1.5555405e-01  +4.5e-09  +5.2e-09  +5.2e-09  +1.0e+00  1.1e+01  3.0e-08 [maximal iteration number reached]
 iter           F     fdiff     mdiff      redf     ratio     Delta      nrmg
   1  +2.9111675e-01  +3.1e-01  +3.6e-01  +4.0e-01  +1.1e+00  1.1e+01  4.8e-02 [linear convergence]
   2  +2.3378994e-01  +4.6e-02  +4.6e-02  +5.7e-02  +1.3e+00  1.1e+01  1.5e-02 [superlinear convergence]
   3  +2.0915478e-01  +2.0e-02  +1.9e-02  +2.5e-02  +1.3e+00  1.1e+01  6.2e-03 [superlinear convergence]
   4  +1.9829458e-01  +9.1e-03  +8.7e-03  +1.1e-02  +1.2e+00  1.1e+01  2.7e-03 [superlinear convergence]
   5  +1.9579412e-01  +2.1e-03  +2.2e-03  +2.5e-03  +1.1e+00  1.1e+01  7.1e-04 [superlinear convergence]
   6  +1.9565850e-01  +1.1e-04  +1.3e-04  +1.4e-04  +1.0e+00  1.1e+01  4.8e-05 [superlinear convergence]
   7  +1.9565804e-01  +3.8e-07  +4.6e-07  +4.6e-07  +1.0e+00  1.1e+01  1.8e-07 [superlinear convergence]

结果分析

注意到实验的设置（精度、共轭梯度法的参数等）与牛顿法相同，并且由于此问题为强凸问题而选择了较大的初始信赖域半径，在数据集 a9a 和 ijcnn1 的求解过程中，信赖域子问题的求解并未因为超出信赖域边界而停机，因此在这两个数据集上信赖域方法的数值表现与牛顿法的表现相同。

同时，从输出的迭代信息中我们看到，在收敛过程中，外层迭代经过几步的线性收敛过程，而后则呈现出超线性收敛速度，这也与图示是相符的。

参考页面

信赖域算法解优化问题的算法请见信赖域方法解优化问题。作为对比，可以参考页面实例：牛顿法解逻辑回归问题。

此页面的源代码请见： demo_lr_tr.m。

版权声明

此页面为《最优化：建模、算法与理论》、《最优化计算方法》配套代码。代码作者：文再文、刘浩洋、户将，代码整理与页面制作：杨昊桐。