初始化函数

在给定波形 $A$ 和采集信号 $y$ 的情况下为迭代进行初始化。我们只给出迭代格式，具体的原理在此省略，参见

C. Ma, X. Liu and Z. Wen, "Globally Convergent Levenberg-Marquardt Method for Phase Retrieval," in IEEE Transactions on Information Theory, vol. 65, no. 4, pp. 2343-2359, April 2019, doi: 10.1109/TIT.2018.2881187.

函数主体

function [ z0, info ] = Ini_C( y, A, times )
tic;
[n,L]=size(A);
m=L*n;

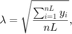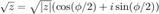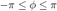$\displaystyle\lambda=\sqrt{\frac{\sum_{i=1}^{nL}y_i}{nL}},$ 注意这里对于复数 $z$ ， $\sqrt{z}=\sqrt{|z|}(\cos(\phi/2)+i\sin(\phi/2))$ 其中 $-\pi\le\phi\le\pi$ 为复数 $z$ 的辐角。

lambda=sqrt(sum(y)/m);
u=ones(n,1);

初始化迭代点。

记 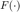$F(\cdot)$ 为一维离散傅里叶变换，记 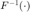$F^{-1}(\cdot)$ 为一维离散逆傅里叶变换，令 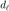$d_\ell$ 为已知的采样信号，令 $b$ 表示观测模长，则

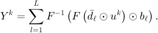
$\displaystyle Y^k=\sum_{l=1}^L F^{-1}\left(F\left( \bar{d}_\ell \odot u^k \right)\odot b_\ell\right).$

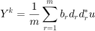事实上，我们有 $\displaystyle Y^k=\frac{1}{m}\sum_{r=1}^mb_rd_rd_r^* u$ （推导略）。

for k=1:times
    Y=zeros(n,1);
    for l=1:L
        Y=Y+A(:,l).*ifft(y((l-1)*n+1:l*n).*fft(conj(A(:,l)).*u))/L;
    end

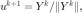$u^{k+1}=Y^k/\|Y^k\|,$ 利用幂法求矩阵 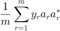$\displaystyle \frac{1}{m}\sum_{r=1}^my_ra_ra_r^*$ 最大特征值对应的特征向量。

    u=Y/norm(Y);
end

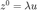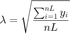初始化的结果为 $z^0=\lambda u$ ，其中 $u$ 为求得的最大特征值对应的特征向量， $\displaystyle \lambda=\sqrt{\frac{\sum_{i=1}^{nL}y_i}{nL}}$ 。返回时间和矩阵向量积的次数。

z0=lambda*u/norm(u);
info.toc=toc;
info.prod=2*times;
end

参考页面

此页面为编码衍射模型的初始化函数，我们在实例：编码衍射模型中展示该模型的一个实例和不同解法在其中的表现。

此页面的源代码请见： Ini_C.m。

版权声明

此页面为《最优化：建模、算法与理论》、《最优化计算方法》配套代码。代码作者：文再文、刘浩洋、户将，代码整理与页面制作：杨昊桐。

初始化函数

目录

函数主体

参考页面

版权声明