实例:非线性最小二乘法的应用――编码衍射模型求解
考虑相位恢复问题:
$$ \min_z f(z):= \frac{1}{2}\displaystyle\sum_{j=(1,1)}^{(n,L)} \left(|\bar{a}_j^\top z|^2-b_j\right)^2, $$
其中 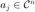 为采样向量。在到编码衍射模型中,则为
为采样向量。在到编码衍射模型中,则为
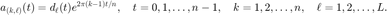
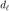 为一系列已知的采样信号,
为一系列已知的采样信号,  为原始信号,
为原始信号, 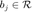 是观测的模长。
是观测的模长。
优化算法解得的  和真实信号
和真实信号  之间可能整体相差一个辐角。 可以利用
之间可能整体相差一个辐角。 可以利用 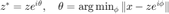 抹掉这个辐角的影响。
抹掉这个辐角的影响。
目录
问题的构建和初始化
读入图片数据,将原始的 0-255 整数转化为 ![$[0,1]$](demo_eq05816708510759450028.png) 浮点数据并向量化,设定随机数生成。
浮点数据并向量化,设定随机数生成。
clear; load('tower.mat'); x_tower = im2double(B1(:)); rng(2020); load('pillar.mat'); x_pillar = im2double(A2(:));
利用信号采集函数 gen_y_c 完成在信号  下的采集,次数为
下的采集,次数为  。
。
L = 20; [y_tower,A_tower]=gen_y_C(x_tower,L); [y_pillar,A_pillar]=gen_y_C(x_pillar,L);
生成迭代的初始点 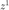 。首先利用函数 Ini_C 生成初始化
。首先利用函数 Ini_C 生成初始化 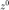 ,然后利用 Nesterov 加速算法进行不超过 100 步的迭代得到
,然后利用 Nesterov 加速算法进行不超过 100 步的迭代得到 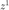 作为各个算法的初始点。 注意到由于提供的信号维度很高,初始化函数耗时可能比较长。
作为各个算法的初始点。 注意到由于提供的信号维度很高,初始化函数耗时可能比较长。
[ z0_tower, ~ ] = Ini_C( y_tower, A_tower, 2000 ); [ z1_tower, ~] = Nes_C( z0_tower, y_tower, A_tower, x_tower, 1e-1,100); [ z0_pillar, ~ ] = Ini_C( y_pillar, A_pillar, 2000 ); [ z1_pillar, ~] = Nes_C( z0_pillar, y_pillar, A_pillar, x_pillar, 1e-1,100);
编码衍射模型求解
分别利用四个算法(Wirtinger 梯度下降方法 WF ,加速版本 Nesterov 算法 Nes , LM方法 ILM1 和采用更精确算法的 LM 方法 ILM2 )对上面构建的编码衍射模型进行求解。 迭代信息以结构体的形式返回。
[ ~, info_wf_tower ] = WF_C( z1_tower, y_tower, A_tower, x_tower, 1e-14 ); [ ~, info_nes_tower ] = Nes_C( z1_tower, y_tower, A_tower, x_tower, 1e-14 ); [ ~, info_ilm_tower ] = LM_C( z1_tower, y_tower, A_tower, x_tower, 0, 1e-14 ); [ ~, info_alm_tower ] = LM_C( z1_tower, y_tower, A_tower, x_tower, 1, 1e-14 ); [ ~, info_wf_pillar ] = WF_C( z1_pillar, y_pillar, A_pillar, x_pillar, 1e-14 ); [ ~, info_nes_pillar ] = Nes_C( z1_pillar, y_pillar, A_pillar, x_pillar, 1e-14 ); [ ~, info_ilm_pillar ] = LM_C( z1_pillar, y_pillar, A_pillar, x_pillar, 0, 1e-14 ); [ ~, info_alm_pillar ] = LM_C( z1_pillar, y_pillar, A_pillar, x_pillar, 1, 1e-14 );
结果可视化
上述算法将迭代过程记录在对应的信息结构体中,将迭代的 cpu 时间和相对误差进行可视化。
fig = figure(1); semilogy(info_wf_tower.time(1:10:end), info_wf_tower.err(1:10:end), '-o', 'Color',[0.99 0.1 0.99], 'LineWidth',2); hold on semilogy(info_nes_tower.time(1:10:end), info_nes_tower.err(1:10:end), '-.*','Color',[0.99 0.1 0.2], 'LineWidth',1.2); hold on semilogy(info_ilm_tower.time, info_ilm_tower.err, '--d','Color',[0.2 0.1 0.99], 'LineWidth',1.5); hold on semilogy(info_alm_tower.time, info_alm_tower.err, ':<','Color',[0.5 0.2 1], 'LineWidth',1.8); legend('WF','Nes','ILM1','ILM2'); xlabel('CPU 时间'); ylabel('$\|z^*-x\|_F/\|x\|_F$','Interpreter','latex'); title('博雅塔'); print(fig,'-depsc','tower.eps'); fig = figure(2); semilogy(info_wf_pillar.time(1:10:end), info_wf_pillar.err(1:10:end), '-o', 'Color',[0.99 0.1 0.99], 'LineWidth',2); hold on semilogy(info_nes_pillar.time(1:10:end), info_nes_pillar.err(1:10:end), '-.*','Color',[0.99 0.1 0.2], 'LineWidth',1.2); hold on semilogy(info_ilm_pillar.time, info_ilm_pillar.err, '--d','Color',[0.2 0.1 0.99], 'LineWidth',1.5); hold on semilogy(info_alm_pillar.time, info_alm_pillar.err, ':<','Color',[0.5 0.2 1], 'LineWidth',1.8); legend('WF','Nes','ILM1','ILM2'); xlabel('CPU 时间'); ylabel('$\|z^*-x\|_F/\|x\|_F$','Interpreter','latex'); title('华表'); print(fig,'-depsc','pillar.eps');
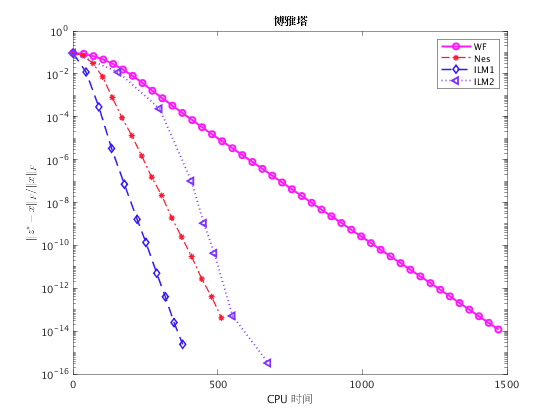

结果分析
上面两图反映了在真实数据分别取博雅图和华表的照片下的四种算法应用于编码衍射模型的收敛情况。 我们发现基本的 WF 方法达到了线性收敛速度。Nesterov 加速方法则在此基础上有较为明显的加速, 在 1/3 的时间内达到了相同的精度。另外,基于 LM 方法的实验也表现出了较好的收敛性, 均快于一般的 WF 方法,其中更为精确的 LM2 方法在略微增加了 cpu 时间的情况下达到了更好的精度。
参考页面
我们利用 Wirtinger梯度下降算法 、 Nesterov加速算法 以及 LM算法 对上面的编码衍射模型进行求解。
另外,信号采集函数详见 编码衍射模型的信号采集 , 迭代初始化函数详见 编码衍射模型的初始化函数。
此页面的源代码请见: demo.m。
版权声明
此页面为《最优化:建模、算法与理论》、《最优化计算方法》配套代码。 代码作者:文再文、刘浩洋、户将,代码整理与页面制作:杨昊桐。
著作权所有 (C) 2020 文再文、刘浩洋、户将