编码衍射模型的 Wirtinger 梯度下降算法

考虑相位恢复问题：

$$ \min_z \;\; f(z)：=\displaystyle\frac{1}{2}\displaystyle\sum_{j=(1,1)}^{(n,L)} \left(|\bar{a}_j^\top z|^2-b_j\right)^2, $$

其中 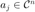$a_j\in\mathcal{C}^n$ 为采样向量。在到编码衍射模型中，则为

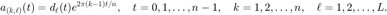
$$ a_{(k,\ell)}(t)=d_\ell(t)e^{2\pi (k-1)t/n},\quad t=0,1,\dots,n-1,\quad k=1,2,\dots,n,\quad\ell=1,2,\dots,L. $$

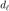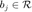$d_{\ell}$ 为一系列已知的采样信号， $x$为原始信号， $b_j\in\mathcal{R}$ 是观测的模长。

目标函数的 Wirtinger 导数为：

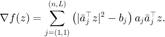
$$ \nabla f(z)=\displaystyle\sum_{j=(1,1)}^{(n,L)} \left( |\bar{a}_j^\top z|^2-b_j \right)a_j\bar{a}_j^\top z. $$

利用 Wirtinger 导数构造梯度下降算法求解相位恢复问题。

目录

初始化和迭代准备

输入信息：迭代初始点 $z_0$，观测模长 $y$，采样信号 $A$，原始数据 $x$ 和停机准则 stop_cri 。 输出信息： 迭代得到的解 $z$（其为真实信号 $x$的恢复），包含迭代信息的结构体 info 。

function [ z, info ] = WF_C( z0, y, A, x, stop_cri)

参数设定，最大迭代次数 2000 次。 $\tau_0$ 和 mumax 为步长相关的参数。

T=cputime;
ite_max=2000;
tau0=330;mumax=0.2;

将向量化的采集信号 $y$ 转化为 $n\times L$ 的矩阵

[n,L]=size(A);
y=reshape(y,n,L);
m=n*L;

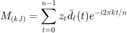计算信号 $z$的在衍射变换下的结果： $M_{(k,l)}=\displaystyle\sum_{t=0}^{n-1}z_t\bar{d}_\ell(t)e^{-i2\pi kt/n}$。 注意到 MATLAB 函数 fft 对于矩阵输入，逐列计算一维的离散傅里叶变换。

rsd=fft(conj(A).*(z0*ones(1,L)));
l=norm(z0,2)^2;
ite=0;
z=z0;

相对误差：

$$ r=\displaystyle\min_{\phi\in[0,2\pi]}\|x-ze^{i\phi}\|_F/\|x\|_F= \|x-ze^{-\theta i}\|_F/\|x\|_F, $$

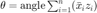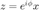其中 $\theta=\mathrm{angle}\sum_{i=1}^n(\bar{x}_iz_i)$ 用表示 $x$ 与 $z$ 之间的夹角。当 $z=e^{i\phi}x$ 时，该相对误差为 $0$。

relerr=norm(x-exp(-1i*angle(trace(x'*z)))*z,'fro')/norm(x,'fro');
info.err=relerr;
info.time=[0];
info.prod=[1];
prod=1;

迭代主循环

达到收敛条件：相对误差 $r$ 小于阈值 stop_cri ， 或者迭代次数超过最大迭代次数 ite_max 限制，停止迭代。

while relerr>stop_cri && ite<ite_max

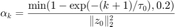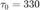第 $k$ 步的步长选取为 $\alpha_k=\displaystyle\frac{\min(1-\exp(-(k+1)/\tau_0),0.2)}{\|z_0\|_2^2}$， 这里 $\tau_0=330$。

    mu=min(1-exp(-(ite+1)/tau0),mumax);
    alpha = mu/l;

由 Wirtinger 导数，有

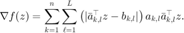
$$ \nabla f(z)=\displaystyle\sum_{k=1}^{n}\sum_{\ell=1}^L \left(|\bar{a}_{k,l}^\top z-b_{k,l}|\right)a_{k,l}\bar{a}_{k,l}^\top z. $$

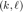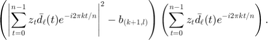
计算矩阵 t，其 $(k,\ell)$ 元素为 $\displaystyle\left(\left|\sum_{t=0}^{n-1}z_t\bar{d}_\ell(t)e^{-i2\pi kt/n}\right|^2-b_{(k+1,l)}\right)\left(\sum_{t=0}^{n-1}z_t\bar{d}_\ell(t) e^{-i2\pi kt/n}\right).$

    t=(abs(rsd).^2-y).*rsd;

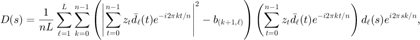
$$ D(s)=\displaystyle\frac{1}{nL}\sum_{\ell=1}^L\sum_{k=0}^{n-1}\left(\left| \sum_{t=0}^{n-1}z_t\bar{d}_\ell(t)e^{-i2\pi kt/n}\right|^2-b_{(k+1,\ell)} \right)\left(\sum_{t=0}^{n-1}z_t\bar{d}_\ell(t)e^{-i2\pi kt/n}\right) d_\ell(s)e^{i2\pi sk/n}, $$

计算梯度 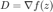$D=\nabla f(z)$。

    D=mean(A.*ifft(t),2);
    % 梯度下降。
    z=z-alpha*D;

迭代步数加一，更新残差的傅里叶变换 rsd 和相对误差 $r$。 更新迭代信息，记录当前步的相对误差、cpu 时间、矩阵向量积次数。

    ite=ite+1;
    rsd=fft(conj(A).*(z*ones(1,L)));
    relerr=norm(x-exp(-1i*angle(trace(x'*z)))*z,'fro')/norm(x,'fro');

    info.err=[info.err,relerr];
    info.time=[info.time,cputime-T];
    prod=prod+2;
    info.prod=[info.prod,prod];
end

当迭代退出时，记录总迭代步。并以 info.state 记录退出原因（是否达到收敛而退出迭代）。

info.ite=ite;
if ite==ite_max
    info.state=0;
else
    info.state=1;
end

end

参考页面

我们在页面 实例：编码衍射模型 中展示了该算法的一个应用，并将其与其它算法进行比较。

此页面的源代码请见： WF_C.m。

版权声明

此页面为《最优化：建模、算法与理论》、《最优化计算方法》配套代码。 代码作者：文再文、刘浩洋、户将，代码整理与页面制作：杨昊桐。

著作权所有 (C) 2020 文再文、刘浩洋、户将


Published with MATLAB® R2020a