信号采集函数
对于输入的信号  利用编码衍射模型,得到其信号采集
利用编码衍射模型,得到其信号采集
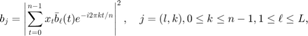
其中 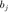 表示采集的波形
表示采集的波形 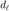 下信号
下信号 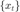 的衍射图的模长。通过改变
的衍射图的模长。通过改变  和对应的波形
和对应的波形 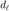 我们生成一系列编码衍射图。
我们生成一系列编码衍射图。
目录
函数主体
函数要求给定信号  和信号采集次数
和信号采集次数  , 返回记录波形的矩阵
, 返回记录波形的矩阵 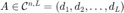 和采集到的信号
和采集到的信号 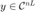 。
。
function [ y, A ] = gen_y_C( x, L )
n=size(x,1);
A=zeros(n,L);
y=zeros(n*L,1);
 为信号采集的次数。
为信号采集的次数。  分别依概率
分别依概率  取
取 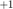 ,
, 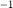 ,
, 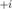 ,
, 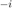 。
。
for k=1:L
b1=zeros(n,1);b2=b1;
b=rand(n,1);
b1(b<0.25)=1;
b1(b>=0.25 & b<0.5)=-1;
b1(b>=0.5 & b<0.75)=-1i;
b1(b>=0.75)=1i;
 依概率
依概率  取
取 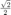 ,依概率
,依概率  取
取 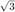 。
。
b=rand(n,1);
b2(b<0.8)=sqrt(2)/2;
b2(b>=0.8)=sqrt(3);
以独立同分布的随机向量 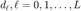 模拟实际场景中的波形, 其中
模拟实际场景中的波形, 其中  。
。
信号采集,利用快速傅里叶变换 fft 函数计算以波形 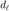 完成上文给定的信号采集,并记录在
完成上文给定的信号采集,并记录在 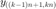 中。
中。
A(:,k)=b1.*b2;
y((k-1)*n+1:k*n)=abs(fft(x.*conj(A(:,k)))).^2;
end
end
参考页面
该函数实现编码衍射模型的信号采集过程,我们在 实例:编码衍射模型 中展示该模型的一个实例。
此页面的源代码请见: gen_y_C.m。
版权声明
此页面为《最优化:建模、算法与理论》、《最优化计算方法》配套代码。 代码作者:文再文、刘浩洋、户将,代码整理与页面制作:杨昊桐。
著作权所有 (C) 2020 文再文、刘浩洋、户将