实例：利用随机优化算法求解逻辑回归问题

考虑逻辑回归问题

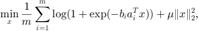
$\displaystyle\min_x \frac{1}{m}\sum_{i=1}^m \log(1+ \exp(-b_ia_i^Tx)) + \mu\|x\|_2^2,$

其中 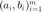$(a_i,b_i)_{i=1}^m$ 为已知的待分类的数据集。

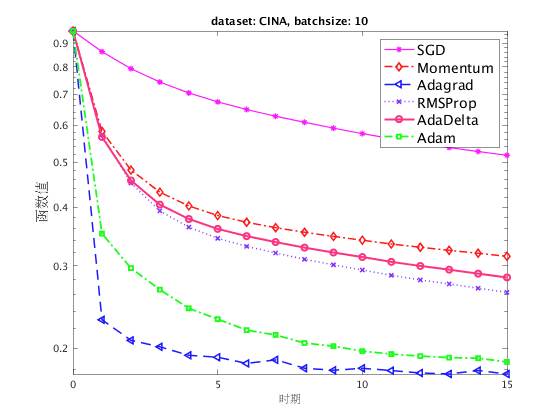
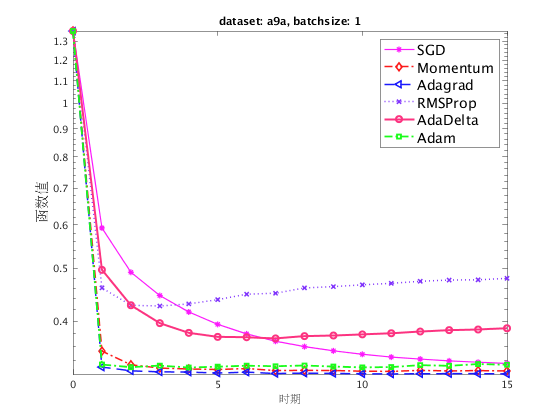
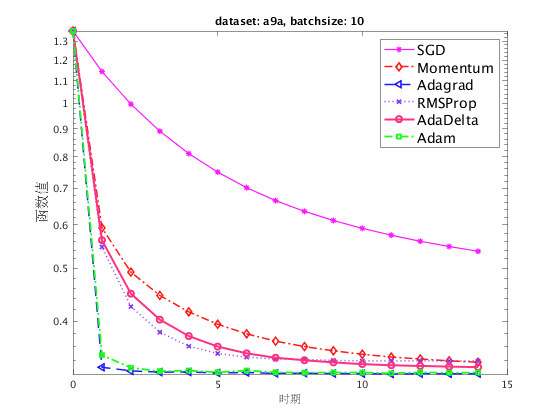
我们测试不同的随机算法（包括SGD, Momentum, Adagrad, RMSProp, AdaDelta 和 Adam），在 LIBSVM 网站上的 CINA 和 a9a 数据集对应的逻辑回归问题的表现。取批量大小 (batchsize) 为 1 和 10 分别进行实验。

测试主体

我们将固定数据集和批量大小的一个测试封装为一个函数 test，并且在两个数据集和两个不同的批量大小下分别调用该函数，完成测试。

clear;

alphalist 用于随机算法的步长格点搜索，当 gs>0 时进行格点搜索。由于格点搜索的耗时较长，在这里我们省略了搜索的过程，直接以预先搜索得到的结果进行展示。

alphalist = [1e-4:3e-4:1e-3, 1e-3:3e-3:1e-2, 1e-2:3e-2:0.1, 0.1:0.1:0.9, 1:1:10,20,40];
gs = 0;
test('CINA.test', 1, alphalist, gs);
test('CINA.test', 10, alphalist, gs);
test('a9a.test', 1, alphalist, gs);
test('a9a.test', 10, alphalist, gs);

格点搜索函数

该函数利用给定的 alphalist ，对给定的数据集、批量和随机算法进行步长的格点搜索。

function [out] = grid_research(alphalist, batchsize, dataset, stoalg, lr_loss, pgfun)

设定随机种子。

seed = 97006855;
ss = RandStream('mt19937ar','Seed',seed);
RandStream.setGlobalStream(ss);

利用预先编译的 libsvmread 函数读取数据集。

[b,A] = libsvmread(dataset);
[N,m] = size(A);

令正则化系数为 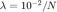$\lambda=10^{-2}/N$ 。

lambda = 1e-2/N;

随机选取迭代初始点，每个实验重复 5 遍，取其平均值。记录最优步长和相应的函数值。

x0 = randn(m,1);
repnum = 5;
alpha_best = 0.1;
fvec_best = inf;

参数的设定。

opts = struct();
opts.batchsize = batchsize;
opts.maxit = 15*N/opts.batchsize;
opts.alpha = 1e1;
opts.step_type = 'fixed';
fun = @(x)lr_loss(x,A,b,lambda);

设定不同的随机算法，通过将 stofun 赋为对应的算法的函数句柄调用对应的算法。

if strcmp(stoalg,'sgd')
    stofun = @sgd;
    opts.momentum = 0;
elseif strcmp(stoalg, 'sgd_m')
    stofun = @sgd;
    opts.momentum = 1;
elseif strcmp(stoalg, 'AdaDelta')
    stofun = @AdaDelta;
elseif strcmp(stoalg, 'Adagrad')
    stofun = @Adagrad;
elseif strcmp(stoalg, 'Adam')
    stofun = @Adam;
elseif strcmp(stoalg, 'RMSProp')
    stofun = @RMSProp;
end

对 alphalist 中的步长进行格点搜索，找到最优步长。在每一个选定的步长下，重复若干次实验，取其平均值。

for alpha = alphalist
    opts.alpha = alpha;
    for i = 1:repnum

调用相应的随机算法进行求解。 out.fvec 记录随机算法的目标函数值变化，这里对重复实验的目标函数值进行累加，并求其平均值。

        [~,out] = stofun(x0,N,@(x, ind)pgfun(x, ind, A, b, lambda),fun,opts);

        if i == 1
            fvec = out.fvec;
        else
            fvec = fvec + out.fvec;
        end

    end
    fvec = fvec / repnum;

如果当前步长下，最后一步的目标函数值比历史最优值更小，则记录当前步长为最优步长，并且记录此步长下的目标函数变化。格点搜索结束后，返回最优步长和此步长下的目标函数变化。

    if fvec(end) < fvec_best(end)
        fvec_best = fvec;
        alpha_best = alpha;
    end
end
out.fvec = fvec_best;
out.alpha_best = alpha_best;
end

测试函数

测试函数完成对于六种随机算法在给定数据集和批量大小下的测试，按照给定的 alphalist 搜索最佳步长，并且对最佳步长下的优化过程予以可视化。

分别对六种随机算法，在给定的数据集和批量大小下测试，寻找最佳步长，并返回在最佳步长下的收敛结果。

function test(dataset, batchsize, alphalist, gs)
if gs
    out1 = grid_research(alphalist, batchsize, dataset, 'sgd', @lr_loss, @pgfun);
    out2 = grid_research(alphalist, batchsize, dataset, 'sgd_m', @lr_loss, @pgfun);
    out3 = grid_research(alphalist, batchsize, dataset, 'Adagrad', @lr_loss, @pgfun);
    out4 = grid_research(alphalist, batchsize, dataset, 'RMSProp', @lr_loss, @pgfun);
    out5 = grid_research(alphalist, batchsize, dataset, 'AdaDelta', @lr_loss, @pgfun); % AdaDelta不需要步长参数。
    out6 = grid_research(alphalist, batchsize, dataset, 'Adam', @lr_loss, @pgfun);
    % 依次输出六种随机算法的最佳步长。
    fprintf('best alpha %.2e, %.2e, %.2e,  %.2e, %.2e\n',out1.alpha_best,...
        out2.alpha_best,out3.alpha_best,out4.alpha_best, out6.alpha_best);

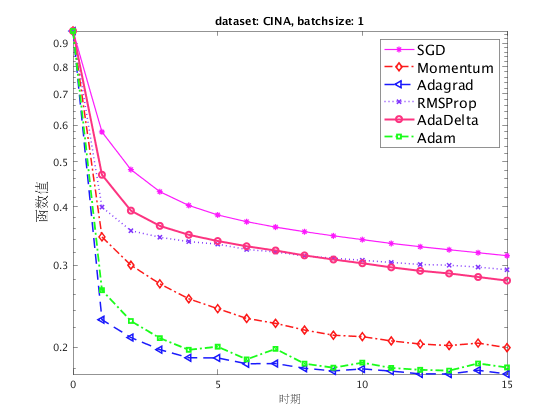
这里我们直接给出经过线搜索得到的最佳步长，以节省时间，特别的由于 sgd 对于步长选取不稳定，这里选择惯用的 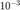$10^{-3}$ 作为默认值。

else
    out1 = grid_research(1e-3, batchsize, dataset, 'sgd', @lr_loss, @pgfun);
    out2 = grid_research(1e-3, batchsize, dataset, 'sgd_m', @lr_loss, @pgfun);
    out3 = grid_research(0.4, batchsize, dataset, 'Adagrad', @lr_loss, @pgfun);
    out4 = grid_research(1e-3, batchsize, dataset, 'RMSProp', @lr_loss, @pgfun);
    out5 = grid_research(1e-3, batchsize, dataset, 'AdaDelta', @lr_loss, @pgfun); % AdaDelta不需要步长参数。
    out6 = grid_research(5e-3, batchsize, dataset, 'Adam', @lr_loss, @pgfun);
end

结果可视化。

fig = figure;
semilogy(out1.epoch, out1.fvec, '-*', 'Color',[0.99 0.1 0.99], 'LineWidth',1.2);
hold on
semilogy(out2.epoch, out2.fvec, '-.d', 'Color',[0.99 0.1 0.1], 'LineWidth',1.5);
hold on
semilogy(out3.epoch, out3.fvec, '--<', 'Color',[0.1 0.1 0.99], 'LineWidth',1.5);
hold on
semilogy(out4.epoch, out4.fvec, ':x', 'Color',[0.5 0.2 0.99], 'LineWidth',1.5);
hold on
semilogy(out5.epoch, out5.fvec, '-o', 'Color',[0.99 0.2 0.5], 'LineWidth',2);
hold on
semilogy(out6.epoch, out6.fvec, '-.s', 'Color',[0.1 0.99 0.1], 'LineWidth',1.8);
hold on
legend('SGD', 'Momentum','Adagrad', 'RMSProp', 'AdaDelta','Adam','fontsize', 14,'Location','northeast');
ylabel('函数值', 'fontsize', 14);
xlabel('时期');
name = sprintf('dataset: %s, batchsize: %d',dataset(1:end-5),batchsize);
title(name);
dir = sprintf('sg-lr-%s-batch-%d.eps', dataset(1:end-5), batchsize);
print(fig, '-depsc',dir);

end

辅助函数

逻辑回归问题的分量梯度，该函数利用 ind 表示一个批量选取的下标，并返回该批量对应的梯度。

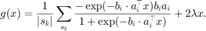
$\displaystyle g(x)=\frac{1}{|s_k|}\sum_{s_k} \frac{-\exp(-b_i\cdot a_i^\top x)b_ia_i}{1+\exp(-b_i\cdot a_i^\top x)}+2\lambda x.$

function g = pgfun(x,ind, A, b, lambda)
bind = b(ind);
Aind = A(ind,:);
Ax = Aind*x;
expba = exp(- bind.*Ax);
g = Aind'*(bind./(1+expba) - bind)/length(ind) + 2*lambda*x;
end

优化问题的目标函数，在数据 $A$ , $b$ , $\lambda$ 和当前点 $x$ 处返回逻辑回归的目标函数值

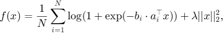
$\displaystyle f(x)=\frac{1}{N}\sum_{i=1}^N \log(1+\exp(-b_i\cdot a_i^\top x))+\lambda||x||_2^2,$

和全部数据对应的梯度

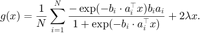
$\displaystyle g(x)=\frac{1}{N}\sum_{i=1}^N \frac{-\exp(-b_i\cdot a_i^\top x)b_ia_i}{1+\exp(-b_i\cdot a_i^\top x)}+2\lambda x.$

function [f,g] = lr_loss(x,A,b,lambda)

[N,~] = size(A);
Ax = A*x;
Atran = A';
expba = exp(- b.*Ax);
f = sum(log(1 + expba))/N + lambda*norm(x,2)^2;
if nargout > 1
    g = Atran*(b./(1+expba) - b)/N + 2*lambda*x;
end

end

结果分析

在上面的四个折线图中，我们展示了在两个数据集和两种不同的批量大小下，各种随机算法的收敛性。注意到对于随机梯度法(SGD)，由于当步长过大时算法表现不够稳定，因此我们直接采用了惯用的 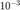$10^{-3}$ 的学习率，而其他算法我们则利用格点搜索搜索到了较为合适的步长。

在选取的特定步长下，这些基于一般的 SGD 而改进的算法得到了更快的下降速度。其中，Adam 和 Adagrad 算法的下降速度最快，并在迭代初期就有非常快的下降速度，这说明自适应步长对于 SGD 性能有着较为明显的提升。同时带动量的 SGD、 RMSProp、 AdaDelta 也都有不错的表现。

同时，也注意到这些随机算法均不是单调算法。

参考页面

在本页面中使用的六个随机算法，参考：随机梯度下降法（包括带动量的sgd）、 AdaGrad、 RMSProp、 AdaDelta、 Adam。

我们在此页面中使用了 LIBSVM 数据集，关于数据集，请参考 LIBSVM 数据集。

此页面的源代码请见： demo_lr_sg.m。

版权声明

此页面为《最优化：建模、算法与理论》、《最优化计算方法》配套代码。代码作者：文再文、刘浩洋、户将，代码整理与页面制作：杨昊桐。