随机梯度下降算法
考虑优化问题:
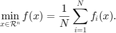
随机梯度下降法(SGD)等概率地抽取选取一个或一组样本 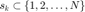 ,并使用如下迭代更新格式:
,并使用如下迭代更新格式:
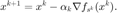
其中, 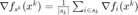 。
。
动量方法在随机梯度下降法基础上引入一个动量变量  ,每次迭代时,利用当前点处的梯度对动量进行更新, 然后以动量作为一步迭代的增量。动量方法的迭代格式如下:
,每次迭代时,利用当前点处的梯度对动量进行更新, 然后以动量作为一步迭代的增量。动量方法的迭代格式如下:
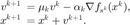
目录
初始化和迭代准备
输入信息:迭代初始值 x0 ,数据集大小 N ,样本梯度计算函数 pgfun ,目标函数值与梯度计算函数 fun 以及提供算法参数的结构体 opts 。
输出信息:迭代得到的解 x 和包含迭代信息的结构体 out 。
- out.fvec :迭代过程中的目标函数值信息
- out.nrmG :迭代过程中的梯度范数信息
- out.epoch :迭代过程中的时期 (epoch)信息。
function [x,out] = sgd(x0,N,pgfun,fun,opts)
从输入的结构体 opts 中读取参数或采取默认参数。
- opts.maxit :最大迭代次数
- opts.alpha :初始步长
- outs.step_type :步长衰减的类型
- outs.batchsize :随机算法的批量大小
- outs.momentum :是否采用动量
- outs.mu :动量的系数
- opts.verbose :不为 0 时输出每步迭代信息,否则不输出
if ~isfield(opts, 'maxit'); opts.maxit = 5000; end if ~isfield(opts, 'alpha'); opts.alpha = 1e-2; end if ~isfield(opts, 'step_type'); opts.step_type = 'fixed'; end if ~isfield(opts, 'batchsize'); opts.batchsize = 10; end if ~isfield(opts, 'momentum'); opts.momentum = 1; end if ~isfield(opts, 'mu'); opts.mu = 0.9; end if ~isfield(opts, 'verbose'); opts.verbose = 1; end
以 x0 为迭代初始点。 计算初始点处的目标函数值和梯度,记初始时期为 0。
x = x0; out = struct(); [f,g] = fun(x); out.fvec = f; out.nrmG = norm(g,2); out.epoch = 0;
 为动量。
为动量。
if opts.momentum v = zeros(size(x)); end
用于计算时期 (epoch) .
count = 1;
迭代主循环
SGD 的迭代循环,以 opts.maxit 为最大迭代次数。
for k = 1:opts.maxit
等概率地从  中选取批量
中选取批量  记录在 idx 之中,批量大小为 opts.batchsize。计算对应的样本的梯度。
记录在 idx 之中,批量大小为 opts.batchsize。计算对应的样本的梯度。
idx = randi(N,opts.batchsize,1);
g = pgfun(x,idx);
选取步长,具体见辅助函数。
alpha = set_step(k,opts);
如果采用带动量的随机梯度下降法(也就动量法),则其迭代格式为
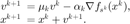
否则,采用标准的随机梯度下降法,即 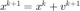 。
。
if opts.momentum v = opts.mu*v - alpha*g; x = x + v; else x = x - alpha*g; end
每当参与迭代的总样本次数超过数据集的总样本时,记为一个时期 (epoch)。 每一个时期,记录当前的目标函数值和梯度范数,并令时期计数增加 1。
if k*opts.batchsize/N >= count [f,g] = fun(x); out.fvec = [out.fvec; f]; out.nrmG = [out.nrmG; norm(g,2)]; out.epoch = [out.epoch; k*opts.batchsize/N]; count = count + 1; end end
end
辅助函数
不同的步长选择,根据 opts.step_type 的不同分别为:
- 'fixed':
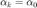
- 'diminishing':
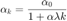
- 'hybrid':
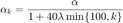
function a = set_step(k, opts) type = opts.step_type; lambda = 0.1; thres_dimin = 100; if strcmp(type, 'fixed') a = opts.alpha; elseif strcmp(type, 'diminishing') a = opts.alpha / (1 + opts.alpha*lambda*k); elseif strcmp(type, 'hybrid') if k < thres_dimin a = opts.alpha / (1 + 40*lambda*k); else a = opts.alpha / (1 + 40*lambda*thres_dimin); end else error('unsupported type.'); end end
参考页面
在页面 实例:利用随机算法求解逻辑回归问题 中,我们展示了该算法的一个应用,并且与其它随机算法进行比较。
其它随机算法参见: AdaGrad、 RMSProp、 AdaDelta、 Adam。
此页面的源代码请见: sgd.m。
版权声明
此页面为《最优化:建模、算法与理论》、《最优化计算方法》配套代码。 代码作者:文再文、刘浩洋、户将,代码整理与页面制作:杨昊桐。
著作权所有 (C) 2020 文再文、刘浩洋、户将